Kezdőlap


Feladat:	B.4175	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Bodor Bertalan , Dinh Hoangthanh Attila , Fonyó Dávid , Hajdók Soma , Hajdók Soma Dániel , Keresztfalvi Tibor , Kiss Melinda Flóra , Mészáros András , Mezei Márk , Milánkovich Dorottya , Nagy Donát , Pálfi Bence , Popper Dávid
Füzet:	2011/május, 277 - 278. oldal		PDF \| MathML
Témakör(ök):	Feladat, Inverzió, Körülírt kör, Thalesz tétel és megfordítása
Hivatkozás(ok):	Feladatok: 2009/április: B.4175

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Végezzünk inverziót, melynek alapköre legyen az $A$ középpontú, $A B$ sugarú kör. A $B$ pont képe így önmaga, a $C$ és $D$ pont képe pedig legyen $C'$ , illetve $D'$ . Az inverzió szögtartó, ezért az $A B C$ és $A B D$ körök inverz alakzatai is merőlegesen fogják egymást metszeni. Mivel mindkét kör átmegy az alapkör középpontján, inverz képük egy-egy egyenes lesz: a $B C'$ és $B D'$ egyenesek. Ezek merőlegesek egymásra, így a $B C' D'$ háromszög derékszögű. Az $A C D$ kör is átmegy az alapkör középpontján, képe a $D' C'$ egyenes, azaz a derékszögű háromszög átfogójának egyenese.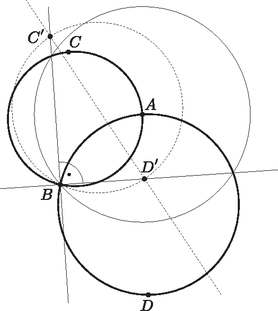

B C D

kör nem megy át az alapkör középpontján, képe így a

B C' D'

kör lesz. Ez a kör a

B C' D'

derékszögű háromszög köré írt köre, ahol az átfogó egyenese (

D' C'

) a Thálesz-tétel szerint egyben a

B C' D'

kör egyik átmérőjének egyenese. A

D' C'

ezek szerint átmegy a

B C' D'

kör középpontján, így az egyenes a kört merőlegesen metszi. Ebből következik, hogy az eredeti körök,

A C D

és

B C D

is merőlegesen metszették egymást.

Hajdók Soma(Budapest, Németh László G.11. évf.)

II. megoldás. Oldjuk meg a feladatot komplex számok segítségével. Az

A

B

C

és

D

pontokba mutató vektoroknak feleljenek meg az

a

b

c

d

komplex számok. Tekintsük az

A B C

háromszöget és annak körülírt körét.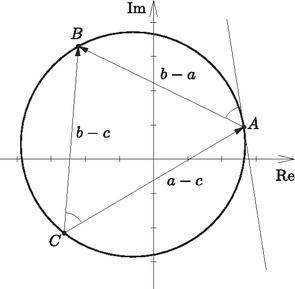

A kerületi szögek tétele miatt az

A

pontba húzott érintő éppen akkora szöget zár be

A B

-vel, mint amekkora a

B C A ∢

. Tehát, ha

(b - a)

-t megszorozzuk

\frac{a - c}{b - c}

-vel, akkor az

A

pontba húzott érintő irányába mutató vektort kapunk:

\frac{a - c}{b - c} (b - a)

. Hasonlóképpen tekintve az

A B D

kört, itt az

A

-hoz húzott érintő iránya megegyezik az

\frac{a - d}{b - d} (b - a)

vektor irányával. E két érintő pontosan akkor merőleges egymásra, ha a két vektor hányadosának

(\frac{(a - c) (b - d)}{(b - c) (a - d)})

valós része 0.
Az

A C D

és a

B C D

körök metszésére ugyanez a feltétel jön ki, így ugyanakkor metszik egymást merőlegesen, mint a fenti két kör.

Mészáros András (Győr, Révay Miklós. G., 11. évf.)