Kezdőlap


Feladat:	B.4250	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Weimann Richárd
Füzet:	2011/április, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Feladat, Ponthalmazok, Szabályos sokszögek geometriája, Műveletek helyvektorok koordinátáival
Hivatkozás(ok):	Feladatok: 2010/február: B.4250

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.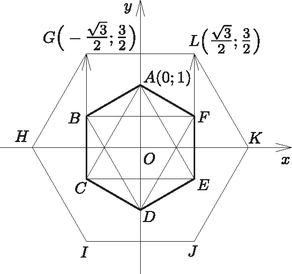

Megoldás. Jelölje a keresett ponthalmazt

H

. A

B F

szakaszt az

\vec{O A}

vektorral eltolva a

G L

szakaszt kapjuk, ahol

G (- \sqrt[]{3} / 2; 3 / 2)

és

L (\sqrt[]{3} / 2; 3 / 2)

. Tehát a

G L

szakasz pontjai a

H

halmazhoz tartoznak. Szimmetriaokok miatt ugyanígy kapjuk, hogy az

O

középpontú

G H I J K L

szabályos hatszög kerületének minden pontja

H

-hoz tartozik, ahol

H (- \sqrt[]{3}; 0)

I (- \sqrt[]{3} / 2; - 3 / 2)

J (\sqrt[]{3} / 2; - 3 / 2)

és

K (\sqrt[]{3}; 0)

1. ábra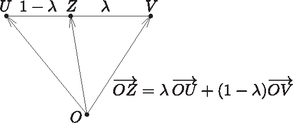

2. ábra

Valamely

K

ponthalmaz pontosan akkor konvex, ha bármely két pontjának összekötő szakaszát is tartalmazza. Ezt vektorok segítségével könnyen leírhatjuk: ha

U, V \in K

0 \leq λ \leq 1

tetszőleges valós szám és

\vec{O Z} = λ \vec{O U} + (1 - λ) \vec{O V}

, akkor

Z \in K

. Ezt felhasználva egyszerűen beláthatjuk, hogy a

H

halmaz konvex. Ha

P, Q \in H

, akkor alkalmas

P_{i}, Q_{i} \in H_{i}

pontokkal

\begin{matrix} \vec{O P} = \vec{O P_{1}} + \vec{O P_{2}} és \vec{O Q} = \vec{O Q_{1}} + \vec{O Q_{2}} \end{matrix}

teljesül. Ezért minden

0 \leq λ \leq 1

szám esetén a

H_{i}

halmazok konvex volta miatt

\begin{matrix} λ \vec{O P} + (1 - λ) \vec{O Q} = (λ \vec{O P_{1}} + (1 - λ) \vec{O Q_{1}}) + (λ \vec{O P_{2}} + (1 - λ) \vec{O Q_{2}}) \in H . \end{matrix}

Tehát

H

tartalmazza a

G H I J K L

hatszöglemez minden pontját.
Megmutatjuk, hogy más pontot viszont nem tartalmaz. Mivel

H_{1}

, illetve

H_{2}

minden pontjának második koordinátája legfeljebb 1, illetve 1/2,

H

minden pontjának második koordinátája legfeljebb 3/2. Tehát

H

egyetlen pontja sincs a

G L

egyenes fölött. Szimmetriaokokból ugyanígy kapjuk, hogy a

G H I J K L

hatszög bármely oldalegyenesének az origót tartalmazó oldalára esik

H

minden pontja.
Tehát a keresett pontok halmaza megegyezik a

G H I J K L

szabályos hatszöglemezzel.