|
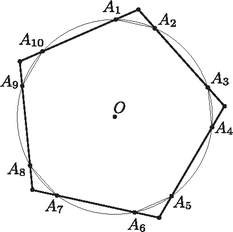
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Vegyünk egy szabályos oldalú sokszöget, majd egy olyan kört, amelynek középpontja a sokszög középpontja, és metszi az oldalakat. A kör és a sokszög metszéspontjai által meghatározott oldalú sokszögre szimmetria okok miatt teljesül, hogy szögei egyenlők, és hogy minden második oldala egyenlő hosszúságú. Most válasszuk meg a kör sugarát akkorára, amekkora az -szög köré írt kör sugara, és kezdjük el csökkenteni a kör sugarát egészen addig, amíg el nem érjük a beírt kört.
Közben kísérjük figyelemmel a oldalú sokszög kétféle oldalának arányát (a nevező legyen az az oldal, amely illeszkedik az oldalú sokszög oldalára). Ez az arány kezdetben nulla, mert a köréírt körtől nagyon kicsit különböző sugarú kör esetében az oldalú sokszög két szomszédos oldalát a közös csúcshoz képest két nagyon közeli pontban metszi, tehát a számláló nagyon kicsi, elfajuló esetben nulla. Majd a végéhez közeledve tart a végtelenhez, mert a beírt körhöz közeli kör egy oldalt két nagyon közeli pontban metszi, azaz a nevező nullához tart. Folytonosan mozgatva így a megfigyelt arány nullától végtelenig minden értéket felvesz, valamikor éppen . Ebben az esetben a metszéspontok által megadott sokszög hasonló az sokszöghöz, mert minden szögük és a megfelelő oldalaik aránya is megegyezik. Az előbbinek van köréírt köre, hiszen úgy származtattuk, ezért az sokszögnek is van.
|
 PDF |
PDF |  MathML
MathML