Feladat:	B.4408	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bingler Arnold ,  Czipó Bence ,  Fehér Zsombor ,  Fonyó Viktória ,  Janzer Olivér ,  Jávorszky Natasa ,  Kaprinai Balázs ,  Kiss Melinda Flóra ,  Lucskai Gábor ,  Machó Bónis ,  Mester Márton ,  Mihálykó András ,  Ódor Gergely ,  Sticza Gergő ,  Strenner Péter ,  Szabó Attila ,  Weimann Richárd
Füzet:	2013/február, 90 - 91. oldal		PDF  |  MathML
Témakör(ök):	Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 2011/december: B.4408

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.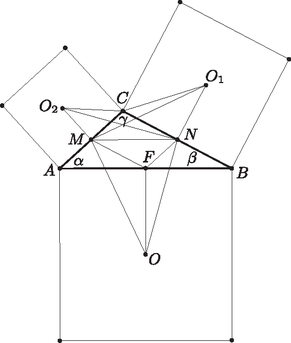   Megoldás. Jelöljük az $ABC$ háromszög oldalait $a$, $b$, $c$-vel, szögeit $\alpha$, $\beta$, $\gamma$ $AB$ oldalának felezőpontját $F$-fel. Állítsunk a háromszög $BC$ és $CA$ oldalaira is kifelé négyzeteket, és jelöljük ezek középpontjait $O_1$, $O_2$-vel.     Felhasználjuk, hogy a háromszög középvonalai párhuzamosak az oldalakkal és fele akkora hosszúságúak, továbbá azt, hogy egy négyzet középpontját egyik oldalfelező ponttal összekötve a kapott szakasz merőleges az adott oldalra, és fele akkora hosszúságú. Ezek szerint ${\displaystyle \begin{array}{cc}\hfill {\displaystyle NFB\sphericalangle }& {\displaystyle =CMN\sphericalangle =CAB\sphericalangle =\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle AFM\sphericalangle }& {\displaystyle =MNC\sphericalangle =ABC\sphericalangle =\beta \mathrm{,}}\hfill \\ \hfill {\displaystyle NFO\sphericalangle }& {\displaystyle =O_{2}MN\sphericalangle ={90}^{\circ }+\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle MFO\sphericalangle }& {\displaystyle =O_{1}NM\sphericalangle ={90}^{\circ }+\beta \mathrm{.}}\hfill \end{array}}$ Így az $ONF$ és $N{O}_{2}M$ háromszögek, továbbá az $OFM$ és $O_{1}NM$ háromszögek egybevágók, mivel két-két oldaluk és az általuk közbezárt szög megegyezik. Az egybevágóság következményeként $ON=N{O}_2=x$ és $OM=M{O}_1=y$. A négyzet átlója az oldallal ${45}^{\circ }$-os szöget zár be, ezért $0^{\circ }<\gamma \le {135}^{\circ }$ esetén $\begin{array}{c}{\displaystyle NC{O}_2\sphericalangle =MC{O}_1\sphericalangle =\gamma +{45}^{\circ }\mathrm{,}}\end{array}$ ${135}^{\circ }<\gamma <{180}^{\circ }$ esetén pedig $\begin{array}{c}{\displaystyle NC{O}_2\sphericalangle =MC{O}_1\sphericalangle ={360}^{\circ }-\left(\gamma +{45}^{\circ }\right)\mathrm{.}}\end{array}$ Felhasználva, hogy a négyzet átlójának fele az oldal hosszának $\frac{\sqrt[]{2}}{2}$-szerese: $\begin{array}{c}{\displaystyle CN=\frac{a}{2}\mathrm{,}CM=\frac{b}{2}\mathrm{,}C{O}_1=\frac{a\sqrt[]{2}}{2}\mathrm{,}C{O}_2=\frac{b\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Másrészt a $\text{cos}\gamma =\text{cos}\left({360}^{\circ }-\gamma \right)$ azonosság alapján a $CM{O}_1$ és a $CN{O}_2$ háromszögekre, vagy elfajuló háromszögekre egységesen az alábbi alakban írható fel a koszinusz-tétel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y^2}& {\displaystyle ={\left(\frac{b}{2}\right)}^2+{\left(\frac{a\sqrt[]{2}}{2}\right)}^2-2\cdot \frac{b}{2}\cdot \frac{a\sqrt[]{2}}{2}\text{cos}\left(\gamma -{45}^{\circ }\right)}\hfill \\ \hfill {\displaystyle x^2}& {\displaystyle ={\left(\frac{a}{2}\right)}^2+{\left(\frac{b\sqrt[]{2}}{2}\right)}^2-2\cdot \frac{a}{2}\cdot \frac{b\sqrt[]{2}}{2}\text{cos}\left(\gamma -{45}^{\circ }\right)\mathrm{.}}\hfill \end{array}}$ A feltételek szerint $a$ és $b$ állandók, az $x^2$ és $y^2$, illetve ezekkel szinkronban az $x$ és $y$ maximumának feltétele, hogy $\text{cos}\left(\gamma +{45}^{\circ }\right)=-1$, azaz $\gamma +{45}^{\circ }={180}^{\circ }$, vagyis $\gamma ={135}^{\circ }$ legyen. Ekkor $\begin{array}{c}{\displaystyle x^2={\left(\frac{a}{2}+\frac{b\sqrt[]{2}}{2}\right)}^2\mathrm{,}{y}^2={\left(\frac{b}{2}+\frac{a\sqrt[]{2}}{2}\right)}^2\mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle x=\frac{a}{2}+\frac{b\sqrt[]{2}}{2}\text{és}y=\frac{b}{2}+\frac{a\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Összegük: $\begin{array}{c}{\displaystyle x+y=\frac{\left(a+b\right)\left(1+\sqrt[]{2}\right)}{2}\mathrm{.}}\end{array}$ Tehát az $ACB$ szöget ${135}^{\circ }$-osnak választva az $OM$ és $ON$ távolságok összegének maximuma $\begin{array}{c}{\displaystyle \frac{\left(AC+BC\right)\left(1+\sqrt[]{2}\right)}{2}\mathrm{.}}\end{array}$