Kezdőlap


Feladat:	B.4311	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Árvay Balázs , Bauer Barbara , Bogár Blanka , Bősze Zsuzsanna , Böőr Katalin , Csahóczi Márton , Dolgos Tamás , Énekes Péter , Halász Dániel , Köpenczei Gergő , Lenger Dániel , Nagy Balázs , Neukirchner Elisabeth , Perjési Gábor , Tekeli Tamás , Zelena Réka
Füzet:	2011/október, 410 - 411. oldal		PDF \| MathML
Témakör(ök):	Feladat, Algebrai átalakítások, Síkgeometriai bizonyítások, Háromszög területe
Hivatkozás(ok):	Feladatok: 2010/november: B.4311

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög magasságait a szokásos módon $m_{a}$ , $m_{b}$ , $m_{c}$ -vel, legyen továbbá a $P$ pontnak az oldalegyenesektől való távolsága rendre $x$ , $y$ és $z$ . Mivel $P$ a háromszög belső pontja,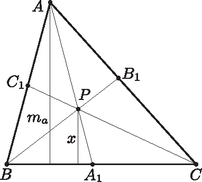

\begin{matrix} T_{A B C} = T_{B C P} + T_{C A P} + T_{A B P} . \end{matrix}

1. ábra

Ebből, felhasználva, hogy közös alapú háromszögek területének aránya megegyezik magasságaik arányával, az

\begin{matrix} 1 = \frac{T_{B C P}}{T_{A B C}} + \frac{T_{C A P}}{T_{A B C}} + \frac{T_{A B P}}{T_{A B C}} = \frac{x}{m_{a}} + \frac{y}{m_{b}} + \frac{z}{m_{c}} . \end{matrix}

(1)

összefüggés adódik.
A párhuzamos szelők tétele szerint viszont:

\begin{matrix} \frac{x}{m_{a}} = \frac{P A_{1}}{A A_{1}} = \frac{P A_{1}}{A P + P A_{1}} = \frac{3}{A P + 3}, \end{matrix}

és ugyanígy

\begin{matrix} \frac{y}{m_{b}} = \frac{3}{B P + 3}, \frac{z}{m_{c}} = \frac{3}{C P + 3} . \end{matrix}

Ezeket beírva az (1) egyenletbe majd rendezve kapjuk, hogy

\begin{matrix} 1 = \frac{3}{A P + 3} + \frac{3}{B P + 3} + \frac{3}{C P + 3}, \\ (A P + 3) (B P + 3) (C P + 3) = \\ = 3 ((B P + 3) (C P + 3) + (A P + 3) (C P + 3) + (A P + 3) (B P + 3)) . \end{matrix}

Ebből pedig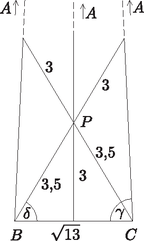

\begin{matrix} A P \cdot B P \cdot C P = \\ = 3 ((A P \cdot B P + B P \cdot C P + C P \cdot A P) + 6 (A P + B P + C P) + 27) - \\ - (3 (A P \cdot B P + B P \cdot C P + C P \cdot A P) + 9 (A P + B P + C P) + 27) = \\ = 9 (A P + B P + C P) + 54 = 9 \cdot 43 + 54 = 441, \end{matrix}

ami épp a bizonyítandó állítás.

Megjegyzés. A feladat megoldásából nem következik, hogy létezik olyan háromszög és a belsejében olyan

P

pont, melyre teljesülnek a feltételek. Ha megpróbálunk ilyet rajzolni, észrevehető, hogy a

P

pont mindhárom oldalhoz aránylag ,,közel'' kell, hogy legyen. A legegyszerűbb példa az az egyenlőszárú háromszög, amelynek alapja

B C = \sqrt[]{13}

, alaphoz tartozó magassága

39

, a

P

pont pedig ezen a magasságon van. Ekkor

A P = 36

és

B P = C P = 3, 5

. A 2. ábrán ennek a háromszögnek az alaphoz közeli része látható.

2. ábra

Az ábrán jelölt szögek

\begin{matrix} γ = arctg 6 \sqrt[]{13} \approx 87, 35^{\circ} és δ = arctg \frac{6}{\sqrt[]{13}} \approx 59, 00^{\circ} . \end{matrix}