Kezdőlap


Feladat:	B.3940	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Éles András , Kunos Ádám , Peregi Tamás , Sümegi Károly , Szalkai Balázs , Szalóki Dávid , Szűcs Gergely , Wolosz János
Füzet:	2010/május, 270 - 273. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 2006/október: B.3940

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $B$ , illetve $D$ csúcsok megtalálásához a négyzet azon tulajdonságát használjuk, miszerint minden csúcs megkapható az $A$ csúcsból az $O$ középpont körüli egymás után vett $90^{\circ}$ -os forgatásokkal.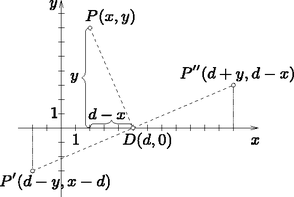
A későbbi tárgyalás egyszerűségéért engedjük meg, hogy a négyzet ponttá fajuljon. Ha ezt nem szeretnék, akkor is egyértelmű, hogy a mértani helyek mely pontjait kell elhagyni.
Ha egy $P (x, y)$ pontot egy $D (d,0)$ pont körül forgatunk $+ 90^{\circ}$ -kal, akkor nyilván a $P' (d - y, x - d)$ pontot kapjuk, ha $- 90^{\circ}$ -kal forgatjuk, akkor pedig a $P'' (d + y, d - x)$ pontot. (Az 1. ábrán látható megfontolásokhoz hasonlóan belátható a többi esetre is.)

1. ábra

Ezek alapján az adódik, hogy egy

a x + b y + c = 0

egyenletű egyenes

+ 90^{\circ}

-os elforgatottja

D

körül:

b x - a y - (a + b) d - c = 0

egyenletű,

- 90^{\circ}

-os elforgatottja pedig:

b x - a y + (a - b) d + c = 0

egyenletű.
Legyen az

o

egyenes egy pontja

O

. Ha létezik hozzá a megfelelő négyzet, akkor legyenek ennek csúcsai

A \in a

C \in c

B

és

D

.
Látható, hogy

D

A

pont

O

körüli

- 90^{\circ}

-os elforgatottja, de

D

C

pont

O

körüli

+ 90^{\circ}

-os elforgatottja is, ami azt jelenti, hogy

D

bizonyosan rajta van

a

- 90^{\circ}

-os és

c

+ 90^{\circ}

-os

O

körüli elforgatottján, tehát a metszéspontjukban van, ha létezik metszéspont (2. ábra). Hasonlóan látható, hogy

B

a

+ 90^{\circ}

-os és a

c

- 90^{\circ}

-os elforgatottjának metszete, ha létezik.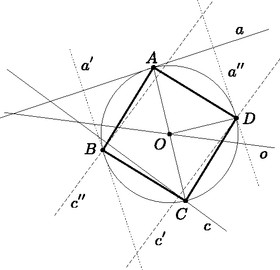

2. ábra

Helyezzük el az

o

egyenest az

x

tengelyen,

a

és

c

egyenesek pedig legyenek

a_{1} x + b_{1} y + c_{1} = 0

és

a_{2} x + b_{2} y + c_{2} = 0

egyenletűek. Vegyünk egy

O (u,0) \in o

pontot.
Az

a

és

c

egyenesek felcserélésével

B

és

D

szerepe is felcserélődik, ezért most csak a

D

pontot vizsgáljuk. Legyen

D

(x, y)

koordinátájú pont. Ekkor, mivel

D

a

egyenes

- 90^{\circ}

-os és a

c

egyenes

90^{\circ}

-os

O

körüli elforgatottjának metszéspontja, az

x

-re és

y

-ra teljesül, hogy

\begin{matrix} b_{1} x - a_{1} y + (a_{1} - b_{1}) u + c_{1} & = 0, \\ b_{2} x - a_{2} y - (a_{2} + b_{2}) u - c_{2} & = 0. \end{matrix}

Ezen egyenletrendszert megoldva adódik, hogy

\begin{matrix} x & = \frac{c_{2} a_{1} + 2 a_{2} a_{1} u + a_{2} c_{1} + b_{2} a_{1} u - b_{1} a_{2} u}{b_{2} a_{1} - b_{1} a_{2}}, \\ y & = \frac{b_{2} a_{1} u + b_{2} c_{1} + b_{1} c_{2} + b_{1} a_{2} u}{b_{2} a_{1} - b_{1} a_{2}}, amennyiben a_{1} b_{2} \neq a_{2} b_{1} . \end{matrix}

Viszont az

\begin{matrix} F = a_{1} b_{2} + a_{2} b_{1}, G = b_{1} a_{2} - b_{2} a_{1} - 2 a_{1} a_{2}, H = c_{1} a_{2} + c_{1} b_{2} + c_{2} b_{1} - c_{2} a_{1} \end{matrix}

számokra

F x + G y + H = 0

minden

O (u,0)

-ra, ami azt jelenti, hogy

D

mértani helye az

F x + G y + H = 0

egyenletű egyenes.
A

B

pont mértani helye nyilván

a_{1}

és

a_{2}

b_{1}

és

b_{2}

, valamint

c_{1}

és

c_{2}

felcserélésével kapható meg.
Ha

a_{1} b_{2} = a_{2} b_{1}

, akkor

a ∥ c

, továbbá az elforgatottak is párhuzamosak. Csak akkor létezik

D

vagy

B

pont, ha egybeesik a két elforgatott, ami nyilván akkor következik be, ha

O

a

és

c

egyenesek középvonalán van, azaz a középvonalnak és

o

-nak van metszéspontja: ekkor

D

és

B

mértani helye az

a

és

c

egyenesek

+ 90^{\circ}

-os elforgatottjai

O

körül.
Ha

o ∥ a ∥ c

, és

o

nem az

a

és

c

egyenesek középvonala, akkor szerkesztési eljárásunk szerint ‐ ami egyértelműen meghatározza a négyzetet, ha az létezik ‐ nyilván nem létezik

B

és

D

, mert az elforgatottak mindig egymástól különböző párhuzamosok. Ha

o

a

és

c

egyenesek középvonala,

D

(és persze

B

) mértani helye az egész sík.

II. megoldás. A négyzet

A

és

C

csúcsa egyenlő távolságra van az

o

egyenestől, ha

O \in o

. Ha tükrözzük

A

-t és a rajta átmenő tetszőleges

a

egyenest az

o

egyenesre, akkor

A'

(az

A

tükörképe) ugyanakkora távolságra lesz

o

-tól, mint

C

. Így a lehetséges

C

és

A'

pontpárok

o

-val párhuzamos egyenest határoznak meg, a hozzájuk tartozó

O

pedig

A'

és

C

felezőmerőlegesének és

o

-nak a metszéspontja lesz. Mivel

A'

tükörképe

a

-n lesz, az

A

pont biztosan

a

-ra illeszkedik, továbbá

B

és

D

is megszerkeszthetőek.
Vegyük a lehetséges

A' C

szakaszok felezőpontjait (feltéve, hogy

o

nem párhuzamos sem

c

-vel, sem

a'

-vel), ezek egy

s

egyenesen helyezkednek el, ugyanis

c

és

a'

egyeneseket egy

o

-val párhuzamos

o_{1}

egyenessel elmetszve kapjuk sorban a

C_{1}

és

A'_{1}

pontokat, illetve az

F_{1}

felezőpontot. Ha

c

és

a'

metszéspontja

M

, akkor minden további

o_{2} ∥ o

egyenessel metszve a

C_{1} M A'_{1} ▵

-höz hasonló

C_{2} M A'_{2} ▵

-t kapunk az

M

középpontú hasonlóság szerint. Ez a hasonlóság viszi

F_{1}

-et

F_{2}

-be. Így a felezőpontok mértani helye az

M F_{1} = s

egyenes. Ha

c

és

a'

párhuzamosak, akkor a felezőpontok

c

és

a'

középpárhuzamosán lesznek.
Nem szerkeszthető

C

ily módon, ha nincs

c

-nek és

o_{1}

-nek metszéspontja:

c ∥ o_{1}

, azaz ha

c ∥ o

. Ekkor az

o_{2} = c

esetben végtelen sok metszéspont jön létre:

c

bármely pontját választhatjuk

C

-nek, melyekhez ugyanazon

A'

tartozik,

c

és

a'

metszéspontja, ha van. Ha

o ∥ c ∥ a'

, akkor

o ∥ c ∥ a

is teljesül, és csak akkor szerkeszthető a négyzet, ha

o

a középpárhuzamosuk. Ugyanígy

A'

az egész

a'

egyenesen választható, ha

a ∥ o

, melyekhez pontosan egy

C

található, ha

a

és

c

nem párhuzamosak, egyébként pedig

o

-nak középpárhuzamosnak kell lennie.
Az

F

felezőpont

o

-ra merőleges vetületeként kapjuk a megfelelő

O

középpontot.
Felhasználjuk, hogy tetszőleges

u

v

w

z

és

x

valós számokkal az

(u x + v, w x + z)

koordinátákkal megadott pontok mértani helye egy egyenes, ha

u

és

w

nem egyszerre 0. Ugyanis ha

u = 0

, akkor az

X

-tengelyre merőleges egyenesen, ha

w = 0

, akkor az

Y

-tengelyre merőleges egyenesen lesznek a pontok (továbbá minden pont ilyen alakú, pl.

(v, y)

pont esetében

x = \frac{y - z}{v}

). Ha

u w \neq 0

, akkor

\begin{matrix} \frac{w}{u} (u x + v) + (z - \frac{v w}{u}) = w x + z \end{matrix}

alapján a pontok egy

\frac{w}{u}

meredekségű, az

Y

-tengelyt

z - \frac{v w}{u}

-ben metsző egyenesen vannak. (Az egyenes minden pontját megkapjuk ily módon: ha

\begin{matrix} P (x_{0}, \frac{w}{u} x_{0} + z - \frac{v w}{u}), \end{matrix}

akkor

x = \frac{x_{0} - v}{u}

számmal megkapjuk a

P

koordinátáit a kívánt módon.)
A megfelelő

B

pontokat az alábbi módon kaphatjuk meg: kijelölünk

s

-en egy pontot, és rajta át párhuzamost húzunk

o

-val. Ahol a párhuzamos metszi

c

-t, ott lesz

C

. A kijelölt pont

o

-ra való merőleges vetülete lesz

O

. A

C

-t

O

körül

- 90^{\circ}

-kal elforgatva kapjuk

B

-t.
Tegyük az egyeneseket egy olyan koordináta-rendszerbe, melynek

X

-tengelyére esik

o

, az origó pedig legyen

o

és

s

metszéspontjában. A

B

pont szerkesztése során csupa olyan transzformációt végzünk, amellyel a kapott pontok koordinátái egy

x

tetszőleges valós szám elsőfokú polinomjaként állnak elő, legyen

x

a kiválasztott pont origótól való távolsága.
Tehát, ha létezik az

s

egyenes, akkor a

B

és

D

pontok mértani helye egy-egy egyenes.
Szerkesztésünk során felbukkant néhány kivételes elrendezés, melyeket külön kell megvizsgálni.
1. Ha

a' ∥ o ∥ c

és

a' \neq c

, akkor nincs megoldás.
2. Ha

o

középpárhuzamos, akkor

c = a' = s

és a sík bármely

P

pontja lehet

B

vagy

D

. Vegyünk ekkor egy tetszőleges

O

pontot

o

-n

P

merőleges vetületén (

T

) kívül. Szerkesszünk merőlegest

O P

-re

O

-n át: ez a merőleges

a

-t és

c

-t

A

-ban és

C

-ben metszi. Ekkor

A O = C O > O P

teljesül, ha

O

elegendően közel van

T

-hez.

O

-t távolítva

T

-től

O A = O C

tart

a

és

c

egyenesek távolságához,

O P

pedig a végtelenhez folytonosan. A folytonosság miatt lesz egy olyan helyzet, amikor

O A = O C = O P

, ebben a helyzetben

P

valóban egy előforduló négyzet

B

csúcsa. Ha

O

-t az

o

-n

T

másik oldalán vesszük fel, akkor

D

csúcsot kapunk.
3.

a ∥ o

vagy

c ∥ o

(és

c

nem párhuzamos velük). A

B

és

D

pontok mértani helye szintén egy-egy egyenes.
4. Bármely két egyenes egybeesésekor csak akkor lesz megoldás a fentiek szerint, ha

a

és

o

vagy

c

és

o

esnek egybe. 2.-höz hasonlóan a sík bármely pontja jó lesz. (Ha nem engedjük meg az egy ponttá elfajuló négyzeteket, akkor az egyenesek közös metszéspontja nem jó.) Ha

a

és

c

egybeesik, akkor megoldást kapunk, ha

o

is egybeesik velük: 2. szerint a sík minden pontja (nem elfajuló esetben a közös egyenes kivételével) jó, azaz

B

és

D

pontok mértani helye. Szintén megoldást kapunk, ha

a = c

és

o

metszi őket, ám ekkor a metszéspont kijelöli

O

-t,

B

és

D

a = c

egyenesre

O

-ban merőleges egyenesen lesznek.

Megjegyzés. Többen félreértették a feladatban feltett kérdést, így csak szerkesztési eljárást adtak arra nézve, hogyan találhatóak meg a négyzet

B

és

D

csúcsai rögzített

O

középpontból és

A

csúcsból kiindulva. Pontvesztést jelentett a hiányos diszkusszió.