Kezdőlap


Feladat:	4110. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boros Csanád Örs , Farkas Márton , Iván Dávid , Laczkó Zoltán Balázs , Lászlóffy András , Lovas Lia Izabella , Maknics András , Mayer Martin János , Tamás Zsolt , Trényi Róbert
Füzet:	2010/január, 42 - 47. oldal		PDF \| MathML
Témakör(ök):	Feladat, Közlekedőedény, Egyenletesen gyorsuló rendszerek
Hivatkozás(ok):	Feladatok: 2008/november: 4110. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Számoljuk ki először gyorsításmentes esetben a víz és az olaj elhelyezkedését! A kicsiny sűrűségkülönbség miatt feltételezhetjük, hogy a víz és az olaj elválasztó felülete az U alakú cső vízszintes részére esik, a függőleges szárakban pedig $h_{v}$ magasan víz, illetve $h_{o}$ magasan olaj található (1. ábra). Mivel a két folyadék teljes hossza 0,4 m, a vízszintes szakasz pedig (ha a hajlatok térfogatát elhanyagoljuk) 0,1 m hosszú, fennáll, hogy $h_{v} + h_{o} = 0, 3$ m, azaz

\begin{matrix} h_{o} = 0, 3 - h_{v} . \end{matrix}

(1)

(Itt és a továbbiakban az SI mértékegységeket az egyszerűség kedvéért nem írjuk ki.)

1. ábra

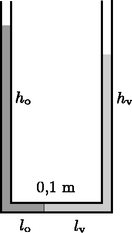Egyensúlyban a két függőleges szárban a hidrosztatikai nyomás megegyezik:

\begin{matrix} ϱ_{o} \cdot g \cdot h_{o} = ϱ_{v} \cdot g \cdot h_{v}, \end{matrix}

ahonnan (1) felhasználásával:

\begin{matrix} 800 (0, 3 - h_{v}) = 1000 h_{v} . \end{matrix}

Ennek megoldásából (három tizedesjegy pontossággal számolva)

\begin{matrix} h_{v} = 0, 133, h_{o} = 0, 166, \end{matrix}

a víz és az olaj szintkülönbségére (a levegővel érintkező folyadékfelszínek magasságkülönbségére) pedig

\begin{matrix} Δ h_{0} = h_{v} - h_{o} = - 0, 033 m, \end{matrix}

vagyis kb. 3,3 cm adódik. (A nullás index a gyorsításmentes esetre utal, a negatív előjel pedig azt fejezi ki, hogy ebben az esetben az olaj áll magasabban.) A vízszintes csőszárban

\begin{matrix} l_{o} = 0, 2 - h_{o} = 0, 033 \end{matrix}

hosszan olaj,

\begin{matrix} l_{v} = 0, 2 - h_{v} = 0, 067 \end{matrix}

méternyi darabon pedig víz található.
A rendszer gyorsítása során a jobb oldali ágban a víz megemelkedik valamekkora

y

értékkel, a bal oldali ágban pedig az olaj lesüllyed (vagy akár el is tűnhet ebből a szárból). Emiatt a vízszintes csőszakasz jobb oldali végénél nagyobb, a bal oldali végénél pedig kisebb lesz a nyomás, mint a fentebb számolt egyensúlyi esetben. A nyomáskülönbségből számolható eredő vízszintes erő hozza létre a vízszintes csőszárban levő folyadék gyorsulását. A továbbiakban három esetet kell megkülönböztessünk.
1. Nem túl nagy gyorsulásnál a folyadékszintek csak kicsit változnak meg, az olaj részben a bal oldali függőleges szárban, részben a vízszintes csőszár egyik darabjában helyezkedik el (2. ábra). Ez

0 < y < 0, 067

vízszintemelkedések esetén teljesül.

2. ábra

2. Közepesen nagy gyorsulásoknál már a jobb oldali függőleges szárba is kerül olaj, de a bal oldali függőleges szár még nem ürül ki teljesen (3. ábra). Ennek feltétele: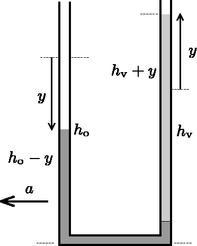

0, 067 < y < 0, 167

3. ábra

3. Nagyon nagy gyorsulásoknál már csak a vízszintes csőszár egy részében és a jobb oldali függőleges szárban található olaj, a bal oldali függőleges szár teljesen kiürül (4. ábra). Ez az eset akkor áll fenn, ha

0, 167 < y < 0, 267

4. ábra

Határozzuk meg a szintkülönbségeket a vízszintes folyadékszakaszra felírt mozgásegyenlet felhasználásával! Az 1. esetben a jobb oldali függőleges csőszár alján

ϱ_{v} g y

-nal megnő, a bal oldali szár alján pedig

ϱ_{o} g y

értékkel lecsökken a nyomás a gyorsításmentes (egyensúlyi) helyzethez képest. Ez a két nyomásváltozás együttesen

\begin{matrix} F = (ϱ_{v} + ϱ_{v}) g y A \end{matrix}

erőt eredményez a vízszintes folyadékra (

A

a cső keresztmetszete). A mozgásegyenlet:

\begin{matrix} (ϱ_{o} + ϱ_{v}) g y A = A [ϱ_{o} (l_{o} + y) + ϱ_{v} (l_{v} - y)] a . \end{matrix}

Ez (az ismert és kiszámított adatok behelyettesítése után)

\begin{matrix} 1, 8 y = [0, 8 (0, 033 + y) + 0, 067 - y] \frac{a}{g} \end{matrix}

alakra hozható, s ebből a

Δ h = 2 y + Δ h_{0}

szintkülönbség kiszámítható:

\begin{matrix} Δ h = 0, 3 \cdot \frac{3 \frac{a}{g} - 1}{\frac{a}{g} + 9} . \end{matrix}

(2)

A fenti képlet érvényességének feltétele

0 < y < 0, 067

; ez pedig

\begin{matrix} 0 < \frac{a}{g} < 1, 5 \end{matrix}

(2a)

esetén teljesül.
A 2. esetben (lásd a 3. ábrát) a vízszintes csődarabban levő

0, 1 \cdot 800 \cdot A

tömegű olajat a jobb oldali szárban levő 0,2 m magas vízoszlop és a

h_{v} + y - 0, 2

magasságú olaj nyomása, valamint a bal oldali szárban levő

h_{o} - y

magas olaj nyomásának különbsége gyorsítja:

\begin{matrix} 0, 1 \cdot 800 A \cdot a = [0, 2 \cdot 1000 + 800 \cdot (h_{v} + y - 0, 2) - 800 \cdot (h_{o} - y)] g A . \end{matrix}

Ebből

y = 0, 05 \frac{a}{g} - 0, 0083

, illetve

\begin{matrix} Δ h = 0, 05 \cdot \frac{a}{g} - 0, 05 \end{matrix}

(3)

adódik. A fenti képlet akkor érvényes, ha

0, 067 < y < 0, 167

, ez pedig

\begin{matrix} 1, 5 < \frac{a}{g} < 3, 5 \end{matrix}

(3a)

gyorsulások esetén teljesül.
Végül vizsgáljuk meg a 4. ábrának megfelelő lehetőséget! A szintkülönbség most éppen a jobb oldali folyadékoszlop magassága:

Δ h = h_{v} + y

, melyből 0,2 méternyi a víz, a többi

Δ h - 0, 2

pedig olaj. A vízszintes csődarabban levő olaj hossza nyilván

0, 4 - Δ h

, így a mozgásegyenlet:

\begin{matrix} [0, 2 \cdot 1000 + (Δ h - 0, 2) \cdot 800] g A = 800 \cdot A (0, 4 - Δ h) a, \end{matrix}

amelyből a szintkülönbség kifejezhető:

\begin{matrix} Δ h = \frac{0, 4 \frac{a}{g} - 0, 05}{1 + \frac{a}{g}} . \end{matrix}

(4)

A fenti összefüggés érvényességi köre

(3 a)

felső határától tetszőlegesen nagy gyorsulásokig terjed, vagyis

\begin{matrix} 3, 5 < \frac{a}{g} < \infty . \end{matrix}

(4a)

Eredményeinket az 5. ábrán látható grafikon foglalja össze, mely a (2), (3), (4) képletek felhasználásával és a

(2 a)

(3 a)

(4 a)

feltételek figyelembe vételével rajzolható meg. A grafikon egy hiperbola-ívből, egy egyenes szakaszból és egy másik hiperbola-ívből áll. Ezek a görbék folytonosan csatlakoznak egymáshoz, de a csatlakozási pontban a meredekségük ugrásszerűen megváltozik.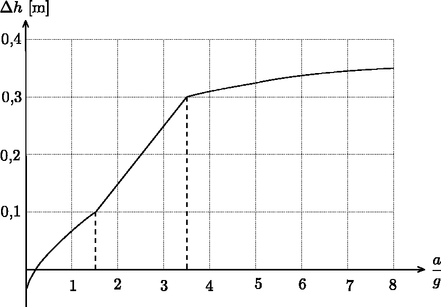

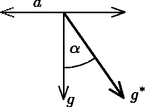5. ábra

II. megoldás. Írjuk le a jelenséget az U alakú csővel együttmozgó, balra gyorsuló koordináta-rendszerből! Ebben a vonatkoztatási rendszerben a függőleges

m g

gravitációs erő mellett minden testre hat még egy vízszintes, jobbra mutató,

m a

nagyságú ,,tehetetlenségi erő'' is. Ezen két erő eredője éppen olyan, mintha a gravitációs gyorsulás

\begin{matrix} g^{*} = \sqrt[]{g^{2} + a^{2}} \end{matrix}

nagyságú lenne, és az iránya a valódi függőlegessel

α

szöget zárna be (6. ábra), ahol

\begin{matrix} tg α = \frac{a}{g} . \end{matrix}

(5)

6. ábra

Határozzuk meg a csőben levő folyadékok egyensúlyi helyzetét abban az esetben, amikor az olaj és a víz határfelülete az U alakú cső alsó, összekötő szakaszára esik. Írjuk fel a hidrosztatikai nyomások egyensúlyi feltételét mondjuk a 7. ábrán látható

O

pontr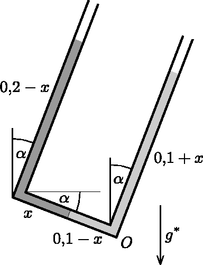a!

7. ábra

Az ábra jelöléseit használva (és a hosszúságokat méterben mérve, de az SI mértékegységeket az egyszerűség kedvéért lehagyva) mondhatjuk:

\begin{matrix} ϱ_{v} g^{*} (0, 1 + x) cos α = ϱ_{v} g^{*} (0, 1 - x) sin α + \\ + ϱ_{o} g^{*} x sin α + ϱ_{o} g^{*} (0, 2 - x) cos α . \end{matrix}

A sűrűségadatok behelyettesítése és

cos α

-val való osztás után kapjuk:

\begin{matrix} 0, 1 + x = (0, 1 - x) tg α + 0, 8 x tg α + 0, 8 (0, 2 - x) . \end{matrix}

Ebből (5) felhasználásával az alsó szárban levő olaj hosszára

\begin{matrix} x = \frac{0, 3 + 0, 5 \frac{a}{g}}{\frac{a}{g} + 9}, \end{matrix}

a folyadékok szintkülönbségére

\begin{matrix} Δ h = (0, 1 + x) - (0, 2 - x) = \frac{0, 9 \frac{a}{g} - 0, 3}{\frac{a}{g} + 9} \end{matrix}

adódik, összhangban az I. megoldás (2) képletével. Ez az összefüggés csak addig érvényes, amíg

x < 0, 1

(vagyis amíg az olaj még nem folyik át a jobb oldali csőszárba); ez pedig

\frac{a}{g} < 1, 5

-re teljesül; egyezően az I. megoldás

(2 a)

feltételével.
Hasonló gondolatmenettel kapjuk meg a (3) és (4) összefüggéseket és

(3 a)

(4 a)

feltételeket is.

Megjegyzés. A megoldás során feltételeztük, hogy a cső keresztmeszete elegendően kicsi ahhoz, hogy az olajat és a vizet ,,folyadékszál'' alakban tartsa, ne engedje összekeveredni azokat. Ez azonban csak kapillárisokra igaz, az 1 cm

^{2}

-es cső pedig nem tekinthető annak. A valóságban az olaj átfolyhat a víz felett a vízszintes csőben, tehát a folyamat a fentebb leírtaktól eltérő módon megy végbe. Ha a megadottnál kisebb keresztmetszetű csövet választunk (a keresztmetszet a számolásból kiesett), akkor érvényesnek vélhetjük a fenti megoldásokat. Sajnos a helyzet még ekkor sem egyszerű! Az olaj átfolyását a kapillaritás akkor akadályozhatja meg, ha a folyadékfelszíneken és a határfelületen a görbületi nyomás összemérhető a hidrosztatikai nyomásokkal; ekkor pedig a kapilláris jelenségeket is figyelembe kellene vegyük a megoldásban.