Kezdőlap


Feladat:	B.4173	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Tamás , Bodor Bertalan , Bősze Zsuzsanna , Csere Kálmán , Damásdi Gábor , Éles András , Énekes Péter , Győrfi Mónika , Huszár Kristóf , Iglói Gábor , Keresztfalvi Tibor , Kiss Melinda Flóra , Lovas Lia Izabella , Mészáros András , Nagy Donát , Nagy Krisztina , Nagy Róbert , Perjési Gábor , Somogyi Ákos , Strenner Péter , Szórádi Márk , Tuan Nhat Le , Weimann Richárd , Weisz Gellért , Zelena Réka
Füzet:	2009/december, 533 - 535. oldal		PDF \| MathML
Témakör(ök):	Feladat, Terület, felszín, Vektorok vektoriális szorzata
Hivatkozás(ok):	Feladatok: 2009/április: B.4173

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel, hogy létezik egy megfelelő $P$ pont. Ekkor $t_{A B P} = t_{A D P}$ , ezért az $A P$ egyenes a $B$ és a $D$ ponttól egyenlő távolságra van, vagyis $m_{1} = m_{2}$ . Ebből következik, hogy a $B M_{1} F$ és a $D M_{2} F$ derékszögű háromszögek egybevágók, így $B F = D F$ , tehát az $A P$ egyenes felezi a $B D$ átlót (1. ábra). Hasonló okok miatt, a $t_{C B P} = t_{C D P}$ egyenlőségéből következik, hogy a $C P$ egyenes is felezi a 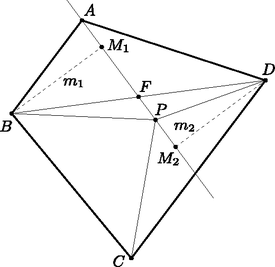$B D$ átlót.

1. ábra

Feltéve, hogy az

A P

és

C P

egyeneseknek egyetlen közös pontja van, az nem lehet más, mint a

B D

átló felezőpontja. Tehát a

P

pont azonos a

B D

átló felezőpontjával.
Mivel

t_{A B P} = t_{B C P}

, illetve

t_{A D P} = t_{C D P}

, azért a

B P

és a

D P

egyenes egyenlő távolságra van az

A

és a

C

ponttól. Mivel

B

P

és

D

egy egyenesre esnek, a

B D

egyenes egyenlő távol van

A

-tól és

C

-től, azaz felezi az

A C

szakaszt.
Ha az

A

P

és

C

pontok esnek egy egyenesbe, akkor az

A C

egyenesre igaz, hogy felezi a

B D

átlót.
Tehát ha a

P

pont létezik, akkor a négyszög egyik átlója felezi a másikat.
Fordítva is igaz: ha a négyszög egyik átlója felezi a másikat, akkor a nem felezett átló felezőpontja megfelel a feltételnek, hiszen a részháromszögek

A P

és

P C

oldalai és a hozzájuk tartozó magasságok is egyenlők (2. ábra).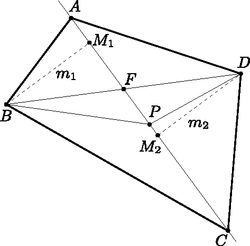

2. ábra

II. megoldás. A háromszög-terület egyenlőségeit felhasználva tudjuk, hogy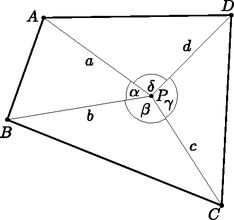

\begin{matrix} a b sin α = b c sin β = c d sin γ = d a sin δ \end{matrix}

(3. ábra), amiből

a b c d sin α sin γ = b a c d sin β sin δ

, vagyis

sin α sin γ = sin β sin δ

3. ábra

Tudjuk, hogy

\begin{matrix} sin α \cdot sin γ = \frac{cos (α - γ) - cos (α + γ)}{2} \end{matrix}

és

\begin{matrix} sin β \cdot sin δ = \frac{cos (β - δ) - cos (β + δ)}{2} . \end{matrix}

Tehát

\begin{matrix} \frac{sin α sin γ}{sin β sin δ} = \frac{cos (α - γ) - cos (α + γ)}{cos (β - δ) - cos (β + δ)} = 1. \end{matrix}

Mivel

α + β + γ + δ = 360^{\circ}

, azért

cos (α + γ) = cos (β + δ)

. Ebből viszont következik, hogy

cos (α - γ) = cos (β - δ)

, amiből a cosinus függvény párosságát figyelembe véve

α - γ = β - δ

vagy

α - γ = δ - β

. Szimmetria-okok miatt elég egyikkel foglalkozni, tehát

α - γ = β - δ

, vagyis

α + δ = β + γ = 180^{\circ}

. Ez azt jelenti, hogy a

P

pont a

B D

átlón helyezkedik el.
Az

α + δ = 180^{\circ}

szerint

α = 180^{\circ} - δ

, így

sin α = sin δ

. Ezt az

a b sin α = d a sin δ

egyenletbe visszahelyettesítve

b = d

adódik. Így a

P

pont a

B D

átló felezőpontja lesz. Ekkor

a b sin α = c d sin γ

-ból

a sin α = c sin γ

, vagyis az

A

és

C

pontok egyenlő távolságra vannak a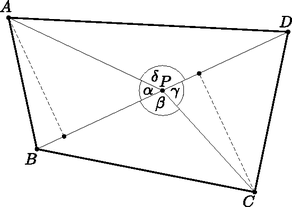

B D

átlótól.

4. ábra

Tehát a feladat feltételét azok a négyszögek elégítik ki, melyeknek van olyan átlójuk, amelytől a másik két csúcs egyenlő távolságra van, és a

P

pont ennek az átlónak a felezőpontjában lesz.