Kezdőlap


Feladat:	B.4153	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Blázsik Zoltán , Botos Csongor , Csere Kálmán , Éles András , Frankl Nóra , Huszár Kristóf , Janosov Milán , Kiss Melinda Flóra , Kunos Vid , Lantos Tamás , Lenger Dániel , Lovas Lia Izabella , Márki Róbert , Márkus Bence , Mester Márton , Perjési Gábor , Somogyi Ákos , Varga László , Weisz Ágoston
Füzet:	2009/október, 410 - 412. oldal		PDF \| MathML
Témakör(ök):	Feladat, Magasságpont, Körülírt kör, Koszinusztétel alkalmazása
Hivatkozás(ok):	Feladatok: 2009/február: B.4153

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a háromszög szögeit a szokásos módon $α$ , $β$ és $γ$ -val, a magaságvonalak talppontjait $T_{A}$ , $T_{B}$ és $T_{C}$ -vel, a körülírt kör sugarát pedig $R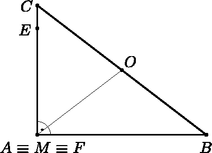$ -rel.
Ha $α = 90^{\circ}$ , akkor $M = A = F$ és az állítás nyilvánvaló (1. ábra). Ha $α$ nem derékszög, akkor megkülönböztetjük az $α < 90^{\circ}$ (2. ábra) és az $α > 90^{\circ}$ (3. ábra) eseteket. Ez utóbbi esetben az $E A F$ háromszög $A$ -nál lévő szöge tompaszög, ezért a vele szemben lévő $E F$ a háromszög legnagyobb oldala. Azaz $E F > A E = A O = R$ , vagyis ekkor a feladat állítása nem igaz. Ha viszont úgy módosítjuk a feladatot, hogy $α > 90^{\circ}$ esetén az $A B C$ háromszög $C A$ oldalának $A$ -n túli meghosszabbításán vesszük fel azt az $E'$ pontot, melyre $A E' = A O = R$ (3. ábra), akkor erre a pontra teljesül, hogy $E' F = A O$ .

1. ábra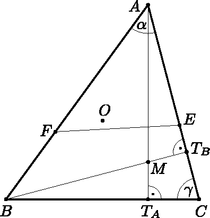

2. ábra

3. ábra

A módosított feladat bizonyítása nagyon hasonló a két esetben, ezért ahol lehet, egyszerre tárgyaljuk a két lehetőséget, de vannak apró eltérések, ezeknél külön-külön kell megvizsgálnunk a hegyes-, illetve a tompaszögű háromszöget.
Az

A B C

háromszögben az általánosított szinusztétel szerint

A B = 2 R sin γ

. Az

A T_{B} B

derékszögű háromszög

B

-nél lévő szöge

90^{\circ} - α

, illetve

α - 90^{\circ}

. Ezért

\begin{matrix} A T_{B} = A B sin (90^{\circ} - α) = 2 R sin γ cos α, \end{matrix}

illetve

\begin{matrix} A T_{B} = A B sin (α - 90^{\circ}) = 2 R sin γ (- cos α) . \end{matrix}

A T_{A} C

derékszögű háromszög

A

-nál lévő szöge

90^{\circ} - γ

. Ez a szög a hegyesszögű esetben egyúttal az

A M T_{B}

derékszögű háromszög

A

-nál lévő szöge is, a tompaszögű esetben pedig

M A T_{B} ∢

és

T_{A} A C ∢

csúcsszögek. Ezért

\begin{matrix} A M = \frac{A T_{B}}{cos (90^{\circ} - γ)} = \frac{2 R sin γ (\pm cos α)}{sin γ} = \pm 2 R cos α . \end{matrix}

Mindkét esetben igaz, hogy

A F = A M

és

A E = A E' = R

. Ha

α

hegyesszög, akkor írjuk fel az

A E F

háromszög

E F

oldalára a koszinusztételt:

\begin{matrix} E F^{2} & = A E^{2} + A F^{2} - 2 A E \cdot A F cos α = \\ = R^{2} + 4 R^{2} cos^{2} α - 2 R \cdot (2 R cos α) \cdot cos α = R^{2}, \end{matrix}

tehát

E F = R

, ami épp a bizonyítandó állítás.
Ha pedig

α

tompaszög, akkor az

A E' F

háromszög

A

-nál lévő szöge

180^{\circ} - α

, ezért ebben a háromszögben a koszinusztétel szerint

\begin{matrix} E' F^{2} & = A E'^{2} + A F^{2} - 2 A E' \cdot A F cos (180^{\circ} - α) = \\ = R^{2} + 4 R^{2} cos^{2} α - 2 R \cdot (- 2 R cos α) \cdot (- cos α) = R^{2}, \end{matrix}

tehát erre a pontra teljesül, hogy

E' F = A O

II. megoldás. Csak hegyesszögű háromszög esetén bizonyítjuk az állítást. (Az olvasóra hagyjuk annak meggondolását, hogy az I. megoldásban kimondott, tompaszögű háromszögekre vonatkozó módosított állítást hogyan lehet a következő bizonyítás apró változtatásával belátni.)
Használjuk az I. megoldás jelöléseit, legyen továbbá az

A B C

háromszög súlypontja

S

, a

B C

oldal felezőpontja

T

, az

E

pontnak az

A B

egyenesen lévő merőleges vetülete pedig

G

. Az

A B C

háromszög körülírt körében a rövidebbik

B C

ívhez tartozó kerületi szög

α

, ezért középponti és a kerületi szögek közti összefüggés alapján

B O C ∢ = 2 α

. Mivel

O

B C

szakaszfelező merőlegesén van,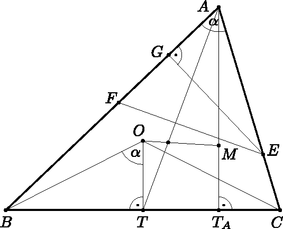

\begin{matrix} B O T ∢ = \frac{B O C ∢}{2} = α . \end{matrix}

Tehát a

B O T

és

E A G

derékszögű háromszögek egybevágóak, mert két-két szögük és az átfogójuk

(B O = R = E A)

megegyezik. Ezért

O T = A G

is teljesül (4. ábra).

4. ábra

Tudjuk, hogy az

O

S

és

M

pontok az

A B C

háromszög Euler-egyenesén vannak és

2 O S = S M

. Az

S O T

és

S M A

(

A B = A C

esetén elfajuló) háromszögek hasonlóak, mert megfelelő oldalaik párhuzamossága (

O T

és

A M

merőleges

B C

-re) miatt a megfelelő szögeik egyenlőek. A hasonlóság aránya

\frac{O S}{S M} = \frac{1}{2}

miatt

1 : 2

, tehát

\begin{matrix} A G = O T = \frac{A M}{2} . \end{matrix}

Vagyis

A G = \frac{A F}{2}

. Mivel

E G

merőleges az

A B

egyenesre, az

A

pont

E G

-re vonatkozó tükörképe

F

. Ebből viszont az is következik, hogy az

E A

szakasz

E G

-re vonatkozó tükörképe az

E F

szakasz.
Tehát

E F = E A = O A

, ami épp a bizonyítandó állítás.