| Feladat: | B.4093 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Kovács Gábor | ||
| Füzet: | 2009/szeptember, 330 - 331. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Sokszög lefedések, Egyenlő szárú háromszögek geometriája, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2008/május: B.4093 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Bármely derékszögű háromszög körülírható körének középpontja az átfogó felezőpontja, ezért ha a háromszög derékszögű csúcsát összekötjük az átfogó felezőpontjával, akkor a háromszög két egyenlőszárú háromszögre bomlik. Minden háromszögre teljesül, hogy a leghosszabb oldalhoz tartozó magasságvonal talppontja az oldal belső pontja, ezért a magasságvonal a háromszöget két derékszögű háromszögre bontja. Tehát tetszőleges háromszög felbontható 4 darab egyenlőszárú háromszögre (1. ábra).  Gondolatmenetünkből az is következik, hogy ha egy háromszög felbontható darab egyenlőszárú háromszögre, akkor ezek közül az egyiket négy részre osztva az eredeti háromszögnek darab egyenlőszárú háromszögre történő felbontását kapjuk. Ezért elegendő az állítást az esetekre bizonyítani. Ezek közül az eset rögtön visszavezethető az imént igazolt esetre, hiszen . Az háromszögre bontást pl. úgy végezhetjük, hogy először berajzoljuk a leghosszabb oldalhoz tartozó magasságot, majd a keletkezett két derékszögű háromszög közül az egyiknek az átfogóhoz tartozó magasságát. Az így kapott három derékszögű háromszög mindegyikét két-két egyenlőszárú háromszögre bontva adódik az eredeti háromszög felbontása 6 darab egyenlőszárú háromszögre (2. ábra). Ha , akkor a legegyszerűbb a háromszöget először tetszés szerint két háromszögre bontani, majd azok mindegyikét tovább bontani 4 egyenlőszárú háromszögre (3. ábra).   Megjegyzés. A felbontások persze nagyon sokféleképpen elvégezhetők. Az esetben talán akkor kapjuk a legegyszerűbb felbontást, ha a beírt kör érintési pontjait összekötjük egymással és a beírt kör középpontjával (4. ábra). 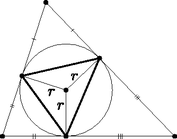 |