Kezdőlap


Feladat:	B.4088	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kiss Melinda Flóra , Kiss Réka
Füzet:	2009/május, 285 - 286. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Magasságvonal, Középpontos és egyéb hasonlósági transzformációk, Vetítések, Magasságpont, Középpontos tükrözés, Helyvektorok, Feladat
Hivatkozás(ok):	Feladatok: 2008/április: B.4088

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy $Q D_{i}$ pontosan akkor merőleges $P F_{i}$ -re, ha $P A$ merőleges $B_{1} B_{2}$ -re. Ebből a feladat állítása nyilván következik.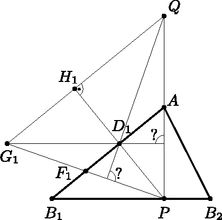
Az $A B_{1} B_{2}$ háromszög hegyesszögű, ezért $D_{i}$ az $A B_{i}$ szakasz belső pontja. Legyen $P$ -nek az $F_{i}$ -re vonatkozó tükörképe $G_{i} .$ Mivel $F_{i}$ felezi a $B_{i} D_{i}$ szakaszt, azért a $P B_{i} G_{i} D_{i}$ négyszög középpontosan szimmetrikus, vagyis paralelogramma. Tehát $G_{i} D_{i}$ párhuzamos $P B_{i}$ -vel, s így $B_{1} B_{2}$ -vel is. Nagyítsuk a $P A F_{i}$ háromszöget $P$ -ből kétszeresére. A nagyításnál $A$ képe $Q,$ $F_{i}$ képe $G_{i}$ , $D_{i}$ képe pedig az a $H_{i}$ pont, amely a $P$ -ből $Q G_{i}$ -re állított merőleges talppontja (lásd ábra).

P Q G_{i}

háromszögben tehát

P H_{i}

magasságvonal. Vizsgáljuk meg, hogy az erre illeszkedő

D_{i}

pont mikor lesz a háromszög magasságpontja. Ez pontosan akkor következik be, ha a háromszögnek még egy magasságvonala átmegy

D_{i}

-n. (Ekkor persze mindhárom magasságvonal átmegy

D_{i}

-n.) A

Q D_{i}

egyenes pontosan akkor magasságvonal, ha

Q D_{i}

merőleges

P G_{i}

-re, azaz

P F_{i}

-re, a

G_{i} D_{i}

egyenes pedig pontosan akkor magasságvonal, ha

G_{i} D_{i}

merőleges

P Q

-ra, azaz ha a

G_{i} D_{i}

-vel párhuzamos

B_{1} B_{2}

merőleges

A P

-re. Vagyis

Q D_{i}

pontosan akkor merőleges

P F_{i}

-re, ha

P A

merőleges

B_{1} B_{2}

-re, mert mindkettő akkor következik be, ha

D_{i}

P Q G_{i}

háromszög magasságpontja.
Ezzel a feladat állítását beláttuk.

II. megoldás. Állításunk bizonyításához indítsunk

A

-ból helyvektorokat és jelöljük ezeket a megfelelő kisbetűkkel, azaz legyen tetszőleges

X

pont esetén

\vec{A X} = x

. Ekkor

Q

és

F_{i}

definíciója miatt

q = - p

és

2 f_{i} = b_{i} + d_{i}

. Mivel

P D_{i}

merőleges

A B_{i}

-re, s így

A D_{i}

-re is, a megfelelő vektorok skaláris szorzata 0, azaz

(p - d_{i}) b_{i} = 0

és

(p - d_{i}) d_{i} = 0

. Vagyis

\begin{matrix} {pb}_{i} = d_{i} b_{i} és {pd}_{i} = d_{i}^{2} . \end{matrix}

(1)

Q D_{i}

szakasz pontosan akkor merőleges

P F_{i}

-re, ha

\begin{matrix} (d_{i} - q) (2 p - 2 f_{i}) = 0, \end{matrix}

amibe behelyettesítve

f_{i}

-t és

q

-t, valamint felhasználva az (1) egyenlőségeket kapjuk, hogy

\begin{matrix} (d_{i} + p) (2 p - b_{i} - d_{i}) & = 0, \\ 2 {pd}_{i} - d_{i} b_{i} - d_{i}^{2} + 2 p^{2} - {pb}_{i} - {pd}_{i} & = 0, \\ ({pd}_{i} - d_{i}^{2}) - (b_{i} d_{i} + {pb}_{i}) + 2 p^{2} & = 0, \end{matrix}

azaz

2 p^{2} = 2 {pb}_{i}

vagyis

p (p - b_{i}) = 0

.
Mivel sem

p

sem

p - b_{i}

nem nullvektor, ez pontosan akkor teljesül, ha a két vektor merőleges egymásra, azaz ha

A P

merőleges

P B_{i}

-re. Tehát

i = 1,2

-re vagy egyszerre merőleges mindkét pár, vagy egyik pár sem merőleges. Ez épp a bizonyítandó állítás. (A bizonyítás során nem használtuk ki, hogy az

A B_{1} B_{2}

háromszög hegyesszögű.)