Kezdőlap


Feladat:	C.868	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Károly Dóra
Füzet:	2007/április, 216 - 217. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Ponthalmazok távolsága, C gyakorlat
Hivatkozás(ok):	Feladatok: 2006/október: C.868

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Először vizsgáljuk azt az esetet, amikor három egységnyi hosszúságú szakasz szabályos háromszöget alkot. Jelöljük e háromszög csúcsait $A$ , $B$ , $C$ -vel. A negyedik pont legyen $A$ -tól 1, $B$ -től 1,2 távolságra. Az $A$ -tól egységnyi távolságra lévő pontok egy körön vannak, hasonlóképpen a $B$ -től 1,2 távolságra lévő pontok is egy körön vannak. A két kör nyilván 2 pontban metszi egymást, legyenek ezek $D$ és $D'$ az ábra szerint. Határozzuk meg mindkét esetben a hiányzó hatodik távolságot.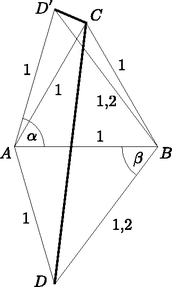

Az első esetben jelöljük az

A B D

szöget

β

-val, és írjuk fel az

A B D

háromszögben a koszinusz-tételt

β

-ra:

\begin{matrix} 1^{2} = 1^{2} + 1, 2^{2} - 2 \cdot 1 \cdot 1, 2 \cdot cos β . \end{matrix}

Innen

cos β = \frac{1, 44}{2, 4} = 0, 6

és

β \approx 53, 13^{\circ}

. Ezután írjuk fel a

D C B

háromszögben a koszinusz-tételt. Itt

C B D ∢ = C B A ∢ + A B D ∢ \approx 60^{\circ} + 53, 13^{\circ} = 113, 13^{\circ}

\begin{matrix} D C^{2} = 1^{2} + 1, 2^{2} - 2 \cdot 1 \cdot 1, 2 \cdot cos 113, 13^{\circ} . \end{matrix}

Innen

D C^{2} \approx 2, 44 + 2, 4 \cdot 0, 3928 = 3, 3827

, és

D C \approx 1, 84

.
A másik esetben a

D' C

távolságot kell meghatároznunk. Jelölje a

D' A B

szöget

α

. Írjuk fel a koszinusz-tételt az

A B D'

háromszögre:

\begin{matrix} 1, 2^{2} = 1^{2} + 1^{2} - 2 \cdot cos α, cos α = \frac{0, 56}{2} = 0, 28, \end{matrix}

innen

α \approx 73, 74^{\circ}

és

D' A C ∢ = α - 60^{\circ} \approx 13, 74^{\circ}

.
Az

A C D'

háromszögben pedig

\begin{matrix} {C D'}^{2} = 1^{2} + 1^{2} - 2 \cdot cos 13, 74^{\circ}, \end{matrix}

azaz

C D' \approx 0, 24

.
Végül, ha az egységnyi szakaszok nem alkotnak háromszöget, akkor egy négyszöget kapunk, melynek egyik átlója 1,2 egység, és minden oldala egységnyi. Mivel a négyszög rombusz, átlói merőlegesen felezik egymást. Felírhatjuk a derékszögű háromszögben a Pitagorasz-tételt: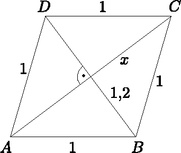

\begin{matrix} x = \sqrt[]{1^{2} - 0, 6^{2}} = 0, 8 és B D = 1, 6. \end{matrix}

A hiányzó hatodik szakasz hossza a pontok elhelyezkedésétől függően 1,84; 0,24 és 1,6 egység lehet.