Kezdőlap


Feladat:	B.3960	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bogár Péter , Csaba Ákos , Fridrik József Richárd , Kardos Kinga Gabriela , Szalóki Dávid , Wolosz János
Füzet:	2008/május, 282. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Hiperbola, mint kúpszelet, Hiperbola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 2006/december: B.3960

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Alkalmas derékszögű koordinátarendszerben a hiperbola egyenlete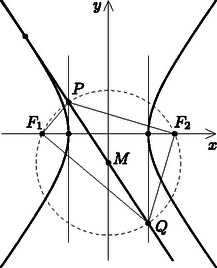

\begin{matrix} \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1. \end{matrix}

Ekkor a fókuszpontok

F_{1} (- \sqrt[]{a^{2} + b^{2}}; 0)

és

F_{2} (\sqrt[]{a^{2} + b^{2}}; 0)

, a valós tengely végpontjai

(- a; 0)

és

(a,0)

, az ezen pontokban a tengelyre állított merőlegesek egyenlete pedig

x = - a

, illetve

x = a

. Legyen a szóban forgó érintő egyenlete

A x + B y = C

. Ekkor az érintés miatt

a^{2} A^{2} - b^{2} B^{2} = C^{2}

(ekkor van a két egyenletnek egy megoldása), a metszéspontok pedig

\begin{matrix} P (- a; \frac{C + a A}{B}), Q (a; \frac{C - a A}{B}), \end{matrix}

ahonnan a

P Q

szakasz felezőpontja

M (0; \frac{C}{B})

Thalész tétele értelmében elegendő azt belátni, hogy a két fókuszpont a

P Q

átmérőjű körvonalra esik, vagyis hogy

M P = M Q = M F_{1} = M F_{2}

. Itt

\begin{matrix} M P^{2} = M Q^{2} = a^{2} + {(\frac{a A}{B})}^{2} és M F_{1}^{2} = M F_{2}^{2} = (a^{2} + b^{2}) + {(\frac{C}{B})}^{2}, \end{matrix}

vagyis a bizonyítandó állítás ekvivalens az

\begin{matrix} a^{2} + \frac{a^{2} A^{2}}{B^{2}} = a^{2} + b^{2} + \frac{C^{2}}{B^{2}} \end{matrix}

egyenlőséggel, amit viszont szorzás és rendezés után a már látott

a^{2} A^{2} - b^{2} B^{2} = C^{2}

alakra hozhatunk.