Kezdőlap


Feladat:	B.3958	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Majoros Csilla
Füzet:	2008/május, 281. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Beírt kör, Tengelyes tükrözés, Középpontos tükrözés, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2006/december: B.3958

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Tükrözzük az $A B C$ háromszöget az $O$ pontra. Az így kapott $A' B' C'$ háromszögnek az $O$ pont szintén a beírható körének középpontja, a beírható köre pedig (mivel az $O$ -ra nézve középpontosan szimmetrikus) közös az eredeti háromszögével.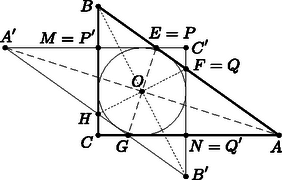
Legyenek az eredeti és a tükrözött háromszög oldalainak metszéspontjai: $E$ , $F$ , $G$ , $H$ , $M$ és $N$ az ábra szerint.

G

pont az

E

pontnak az

O

-ra való tükörképe, mert

E

A B

és

A' C'

egyenesek metszéspontja, míg

G

e két egyenes tükörképeinek metszéspontja. Ugyanígy tükörképe az

O

pontra

F

-nek a

H

és

M

-nek az

N

pont.
Az

A E A' G

és

B F B' H

négyszögek a középpontos tükrözés miatt paralelogrammák és érintik a háromszögek közös beírt körét, tehát érintőnégyszögek is, ezért mindkettő rombusz, vagyis átlóik merőlegesek egymásra.
Tehát

A A' ⊥ E G

, amiből

E O A ∢ = 90^{\circ}

, vagyis az

E

pont a feladatban szereplő

P

ponttal egyezik meg. Hasonlóan

B B' ⊥ F H

, amiből

F O B ∢ = 90^{\circ}

, vagyis az

F

pont megegyezik a

Q

ponttal.
A középpontos tükrözés miatt a

C M C' N

négyszög téglalap és egyben érintőnégyszög, tehát négyzet, vagyis a

P

és

Q

pontoknak a háromszög oldalaira eső merőleges vetületei:

P' = M

és

Q' = N

. Ezek egymás tükörképei az

O

pontra, tehát

P'

O

és

Q'

nemcsak egy egyenesre esnek, hanem

O

éppen a

P' Q'

szakasz felezőpontja.