Kezdőlap


Feladat:	B.3910	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási Gábor András , Cseh Ágnes
Füzet:	2006/december, 544 - 546. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Pitagorasz-tétel alkalmazásai, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 2006/április: B.3910

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha az $E$ pont az $A B$ szakaszon helyezkedik el, akkor $A C = D B = A B$ , vagyis a kifejezés értéke $A B (A E + B E) = A B^{2}$ . Ha $E$ nincs az $A B$ szakaszon, akkor legyen $D A B ∢ = α$ és $C B A ∢ = β$ . Thalész tétele szerint az $A D B$ és $A C B$ háromszögek derékszögűek. Ezért $A D = A B cos α$ , $A C = A B sin β$ , $B C = A B cos β$ és $B D = A B sin α$ . Az $A E B$ háromszög $E$ -nél lévő külső szöge: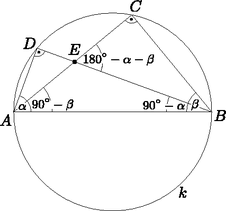

\begin{matrix} D E A ∢ & = C E B ∢ = E A B ∢ + E B A ∢ = \\ = 90^{\circ} - β + 90^{\circ} - α = 180^{\circ} - α - β \end{matrix}

(1. ábra). Ezért az

A D E

és a

B C E

derékszögű háromszögekben:

\begin{matrix} A E = \frac{A D}{sin (180^{\circ} - α - β)} = \frac{A D}{sin (α + β)} = \frac{A B cos α}{sin (α + β)} \end{matrix}

és

\begin{matrix} B E = \frac{B C}{sin (180^{\circ} - α - β)} = \frac{B C}{sin (α + β)} = \frac{A B cos β}{sin (α + β)} . \end{matrix}

Tehát

\begin{matrix} A C \cdot A E + B D \cdot B E & = \frac{A B sin β \cdot A B cos α}{sin (α + β)} + \frac{A B sin α \cdot A B cos β}{sin (α + β)} = \\ = \frac{A B^{2} (sin β cos α + sin α cos β)}{sin (α + β)} = A B^{2} . \end{matrix}

1. ábra

A feladatban szereplő kifejezés értéke tehát

E

helyzetétől függetlenül mindig

A B^{2}

II. megoldás. Abban az esetben adunk újabb megoldást, ha

E

nincs az

A B

szakaszon. Használjuk a 2. ábra jelöléseit. Thalész tételéből következik, hogy az

A D B

A D E

A C B

és

E C B

háromszögek derékszögűek. Ezért Pitagorasz tétele teljesül rájuk. Ezt alkalmazva az első és a második, illetve a harmadik és a negyedik háromszögre:

\begin{matrix} A B^{2} & = e^{2} + {(c + d)}^{2} = a^{2} - c^{2} + (c^{2} + d^{2} + 2 c d) = a^{2} + d^{2} + 2 c d, \\ A B^{2} & = f^{2} + {(a + b)}^{2} = d^{2} - b^{2} + (a^{2} + b^{2} + 2 a b) = d^{2} + a^{2} + 2 a b . \end{matrix}

A két egyenletet összeadva kapjuk, hogy:

\begin{matrix} 2 A B^{2} = 2 a^{2} + 2 d^{2} + 2 a b + 2 c d = 2 (a (a + b) + d (d + c)) = 2 (A C \cdot A E + B D \cdot B E) . \end{matrix}

2. ábra

A C \cdot A E + B D \cdot B E

értéke tehát

E

helyzetétől függetlenül mindig megegyezik a kör átmérőjének négyzetével.

Megjegyzés. Könnyen igazolható, hogy a feladat állítása, tehát hogy

A C \cdot A E + B D \cdot B E = A B^{2}

abban az esetben is teljesül, ha

E

a kör síkjának tetszőleges pontja.