Kezdőlap


Feladat:	B.4026	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balla Attila , Blázsik Zoltán , Bodor Bertalan , Bohus Kinga , Botos Csongor , Dinh Hoangthanh Attila , Dinh Van Anh , Éles András , Fonyó Dávid , Grósz Dániel , Gyurcsik Judit , Hursán Zsófia , Marák Károly , Mészáros András , Nagy Donát , Nagy-Baló András , Pasztuhov Anna , Peregi Tamás , Perjési Gábor , Rácz Tamás , Strenner Péter , Szabó Dávid , Szalkai Balázs , Tossenberger Anna , Varga László , Véges Márton
Füzet:	2008/április, 218 - 220. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Thalesz tétel és megfordítása, Középponti és kerületi szögek, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 2007/október: B.4026

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Először lássunk be egy segédtételt: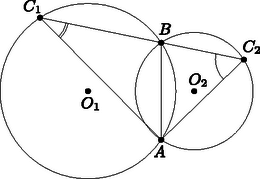
Két metsző kör egyik metszéspontján átmenő tetszőleges egyenesnek a körökön belül fekvő darabja a másik metszéspontból mindig egyenlő (az egyenes irányától független) szögben látszik.
Az 1. ábrán az egy és a két ívvel jelölt szögek a szelő tetszőleges helyzete esetében ugyanakkorák, mivel ugyanazon ívhez tartozó kerületi szögek, így a háromszög harmadik szöge is állandó.

1. ábra

A 2. ábra szerint jelöljük a két kör közös húrjának végpontjait

A

-val és

B

-vel, a

C_{1} D_{1}

és

C_{2} D_{2}

egyenesek metszéspontját

E

-ve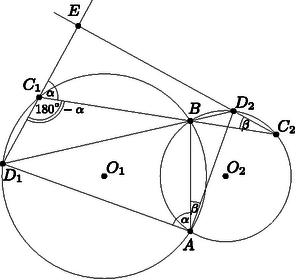l.

2. ábra

Először tegyük fel, hogy

C_{1} D_{1}

merőleges

C_{2} D_{2}

-re.
Ekkor az

E C_{1} C_{2} ∢ = α

és

C_{1} C_{2} E ∢ = β

jelöléseket bevezetve az

E C_{1} C_{2}

derékszögű háromszögben

α + β = 90^{\circ}

. Nyilván

B C_{1} D_{1} ∢ = 180^{\circ} - α

és az

A B C_{1} D_{1}

húrnégyszögben

\begin{matrix} D_{1} A B ∢ = 180^{\circ} - B C_{1} D_{1} ∢ = α . \end{matrix}

Másrészt

B A D_{2} ∢ = B C_{2} D_{2} ∢ = β

, hiszen azonos

B D_{2}

ívhez tartozó kerületi szögek az

O_{2}

középpontú körben.
Így

\begin{matrix} D_{1} A D_{2} ∢ = D_{1} A B ∢ + B A D_{2} ∢ = α + β = 90^{\circ} . \end{matrix}

A segédtétel szerint bármely

B

ponton keresztül húzott szelőnek a két körbe eső darabja az

A

pontból derékszög alatt látszik.
Húzzuk meg ezen szelők közül azt, amelyik merőleges az

A B

húrra, és jelöljük a körökkel alkotott metszéspontokat

M_{1}

M_{2}

-vel (3. 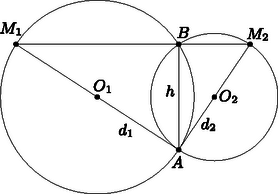ábra).

3. ábra

Mivel a

B

pontból az

A M_{1}

és

A M_{2}

húrok

90^{\circ}

-os szög alatt látszanak, a Thálesz-tétel miatt ezek átmérők a megfelelő körökben.
Az

A B M_{1}

és

A B M_{2}

derékszögű háromszögekre alkalmazva a Pitagorasz-tételt:

\begin{matrix} B M_{1} = \sqrt[]{d_{1}^{2} - h^{2}} és B M_{2} = \sqrt[]{d_{2}^{2} - h^{2}} . \end{matrix}

M_{1} A M_{2}

derékszögű háromszögben a magasságtétel alapján:

\begin{matrix} \sqrt[]{d_{1}^{2} - h^{2}} \cdot \sqrt[]{d_{2}^{2} - h^{2}} = h^{2} . \end{matrix}

Négyzetreemelés után:

(d_{1}^{2} - h^{2}) (d_{2}^{2} - h^{2}) = h^{4}

, amiből

d_{1}^{2} d_{2}^{2} = d_{1}^{2} h^{2} + d_{2}^{2} h^{2}

, illetve osztva a

d_{1}^{2} d_{2}^{2} h^{2} >

0 mennyiséggel:

\begin{matrix} \frac{1}{h^{2}} = \frac{1}{d_{1}^{2}} + \frac{1}{d_{2}^{2}} . \end{matrix}

Megfordítva az állítást, ha

\begin{matrix} \frac{1}{h^{2}} = \frac{1}{d_{1}^{2}} + \frac{1}{d_{2}^{2}} \end{matrix}

egyenlőség teljesül, a levezetést lépésről lépésre visszafele végrehajtva a

B A = \sqrt[]{B M_{1} \cdot B M_{2}}

összefüggés adódik, ami a magasságtétel megfordításaként azt jelenti, hogy

M_{1} A M_{2} ∢ = 90^{\circ}

.
A bizonyított segédtétel alapján így

D_{1} A D_{2} ∢ = 90^{\circ}

, illetve a korábbi levezetés alapján

\begin{matrix} 90^{\circ} = D_{1} A D_{2} ∢ = D_{1} A B ∢ + B A D_{2} ∢ = E C_{1} C_{2} ∢ + C_{1} C_{2} E ∢ . \end{matrix}

Így

C_{2} E C_{1} ∢ = 180^{\circ} - (E C_{1} C_{2} ∢ + C_{1} C_{2} E ∢) = 90^{\circ}