| Feladat: | C.907 | Korcsoport: 16-17 | Nehézségi fok: könnyű |
| Megoldó(k): | Orbán Réka , Szikszay László | ||
| Füzet: | 2008/április, 209 - 210. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai számítások trigonometria nélkül, Négyzetek, Trapézok, Két pont távolsága, szakasz hosszúsága, C gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 2007/szeptember: C.907 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelölje , , és az , , és szakaszok felezőpontját. A feladat szövege szerint: 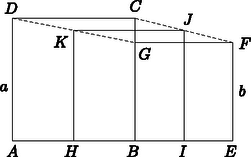 Felhasználjuk, hogy a trapéz középvonala (a trapéz szárainak felezőpontját összekötő szakasz) párhuzamos az alapokkal, hossza pedig az alapok összegének felével egyenlő. Tudjuk, hogy , mert ez a négyzetek közös oldala, , mert ezek a megfelelő négyzetek szemköztes oldalai. Ezért az és az négyszögek olyan trapézok, amelyekben az alapok , . Így a középvonalak hossza is egyenlő: Mivel a trapézok középvonalai párhuzamosak az alapokkal, azért . Hasonlóan és , , így egy olyan trapéz középvonala, amelynek alapjai és hosszúak. Tehát Mivel a négyszögben , és a négyszög szögei -osak, ez a négyszög négyzet, melynek területe: . 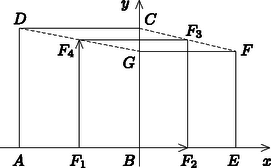 Az négyzet oldalú, így a csúcsok koordinátái: , , , , ahol . A négyzet oldalú, így a csúcsok koordinátái: , , , , ahol . Számoljuk ki a megfelelő felezőpontok koordinátáit. Az felezőpontja: , a felezőpontja: , az felezőpontja: , a felezőpontja: . Ekkor: Hasonlóan számolható, hogy: |