Kezdőlap


Feladat:	2003. évi Eötvös fizikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2004/március, 171 - 174. oldal		PDF \| MathML
Témakör(ök):	Hosszú egyenes vezető mágneses tere, Eötvös Loránd (korábban Károly Irén)
Hivatkozás(ok):	Feladatok: 2004/március: 2003. évi Eötvös fizikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A 3. ábra a két párhuzamos vezető által létesített mágneses tér néhány indukcióvonalát szemlélteti, amikor a vezetőkön egyenlő nagyságú, de ellentétes irányú áramok haladnak át.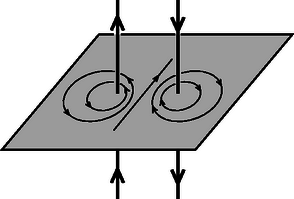

3. ábra

A speciális árameloszlás miatt a létrejövő mágneses mező nagymérvű szimmetriát mutat: az egyik és másik áramvezetőt körülölelő indukcióvonalak nemcsak egymás tükörképei, de akármelyik zárt görbe, amely mentén egy indukcióvonal halad, szimmetrikus a két áramvezetőn átfektetett síkra is. Ettől persze még lehetnek ellipszisek, körök vagy magasabb rendű zárt görbék is az indukcióvonalak, de ha van köztük kör, akkor annak a középpontja benne kell legyen az áramvezetőkön átfektetett síkban.
Vegyünk fel a kiválasztott síkban egy

(x; y)

koordináta-rendszert úgy, hogy az egyik áram az origón, a másik pedig a

(d; 0)

ponton döfje át a síkot. A síkban kiválasztott

P (x; y)

ponton átmenő körök közül tehát csak azok jöhetnek szóba indukcióvonalként, amelyek középpontja rajta van az

x

tengelyen. Egy ilyen kör középpontja legyen az

(x_{0}; 0)

pont. A kör egyenlete ekkor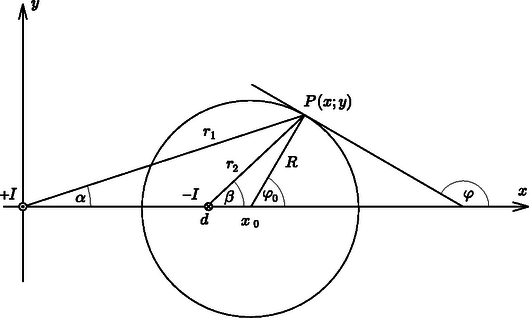

\begin{matrix} {(x - x_{0})}^{2} + y^{2} = R^{2}, \end{matrix}

ahol

R

d

-től és

x_{0}

-tól függő mennyiség.

4. ábra

5. ábra

Ha ez a kör indukcióvonal, akkor az indukcióvektor állása a kör bármely pontjában megegyezik az ottani érintő állásával (4. ábra). A

P (x; y)

ponton átmenő érintő iránytangense:

\begin{matrix} tg φ = - \frac{1}{tg φ_{0}} = - \frac{1}{\frac{y}{x - x_{0}}} = - \frac{x - x_{0}}{y} . \end{matrix}

Ezt kell majd összevetnünk a

P

pontbeli indukcióvektoron átfektetett egyenes iránytangensével. Az eredő

B

iránytangense (5. ábra):

\begin{matrix} tg φ_{B} = \frac{B_{y}}{B_{x}} = \frac{B_{1 y} + B_{2 y}}{B_{1 x} + B_{2 x}} . \end{matrix}

Határozzuk meg ezt a mennyiséget! Egyetlen egyenes vezető által keltett indukcióvektor nagysága:

\begin{matrix} B = \frac{μ_{0} I}{2 π} \cdot \frac{1}{r} . \end{matrix}

Ennek és az 5. ábráról leolvasható geometriai összefüggéseknek a felhasználásával az egyes összetevők:

\begin{matrix} B_{1 y} & = & B_{1} cos α = \frac{μ_{0} I}{2 π} \cdot \frac{cos α}{r_{1}} = \frac{μ_{0} I}{2 π} \cdot \frac{x}{r_{1}^{2}}, \\ B_{2 y} & = & - B_{2} cos β = - \frac{μ_{0} I}{2 π} \cdot \frac{cos β}{r_{2}} = \frac{μ_{0} I}{2 π} \cdot \frac{(d - x)}{r_{2}^{2}}, \\ B_{1 x} & = & - B_{1} sin α = - \frac{μ_{0} I}{2 π} \cdot \frac{sin α}{r_{1}} = - \frac{μ_{0} I}{2 π} \cdot \frac{y}{r_{1}^{2}}, \\ B_{2 x} & = & B_{2} sin β = \frac{μ_{0} I}{2 π} \cdot \frac{sin β}{r_{2}} = \frac{μ_{0} I}{2 π} \cdot \frac{y}{r_{2}^{2}} . \end{matrix}

Helyettesítsük be ezeket a kifejezéseket a

tg φ_{B}

-re felírt összefüggésbe! Egyszerűsítés után:

\begin{matrix} tg φ_{B} = \frac{\frac{x}{r_{1}^{2}} + \frac{d - x}{r_{2}^{2}}}{- \frac{y}{r_{1}^{2}} + \frac{y}{r_{2}^{2}}} = \frac{x (\frac{1}{r_{1}^{2}} - \frac{1}{r_{2}^{2}}) + \frac{d}{r_{2}^{2}}}{- y (\frac{1}{r_{1}^{2}} - \frac{1}{r_{2}^{2}})} = - \frac{x - \frac{d}{1 - {(r_{2} / r_{1})}^{2}}}{y} . \end{matrix}

Ez a kifejezés akkor és csak akkor egyenlő a korábban kapott

\begin{matrix} tg φ = - \frac{x - x_{0}}{y} \end{matrix}

képlettel, ha

\begin{matrix} x_{0} = \frac{d}{1 - {(r_{2} / r_{1})}^{2}} . \end{matrix}

Behelyettesítve az

r_{2} = \sqrt[]{y^{2} + {(x - d)}^{2}}

és

r_{1} = \sqrt[]{y^{2} + x^{2}}

kifejezéseket, rendezés után a következőt kapjuk:

{(x - x_{0})}^{2} + y^{2} = x_{0} (x_{0} - d)

. Ez pedig pontosan a megadott

P

ponton is átmenő,

(x_{0}; 0)

középpontú kör egyenlete, vagyis ez az indukcióvonal kör alakú! Megkaptuk a kör sugarát is:

\begin{matrix} R = \sqrt[]{x_{0} (x_{0} - d)} . \end{matrix}

Íme, ebben a mágneses mezőben minden indukcióvonal kör alakú, hiszen

P

a tér tetszőleges pontja lehet. Egy ponton csak egyetlen indukcióvonal mehet át, az pedig kör alakú.

Megjegyzések. 1. A síkban azoknak a pontoknak a mértani helye, melyek két adott ponttól vett távolságainak aránya állandó, az ún. Apollóniosz-kör. Eredményeinket úgy is megfogalmazhatjuk, hogy a vizsgált mágneses térben az indukcióvonalak Apollóniosz-körök.
Bevezetve az

r_{2} / r_{1} = λ

jelölést, e körök egyenlete

\begin{matrix} {(x - \frac{d}{1 - λ^{2}})}^{2} + y^{2} = {(λ \frac{d}{1 - λ^{2}})}^{2}, \end{matrix}

amiből többek között az

R = λ x_{0}

érdekes összefüggés is leolvasható. (Apollóniosz időszámításunk kezdete előtt 262-től 190-ig élt; a kúpszeletekről írt munkájában ő vezette be az ellipszis, parabola és hiperbola kifejezéseket.)
2. Ha csak kicsit is általánosabb esetet vizsgálunk, a számolás meglehetősen elbonyolódik, és soha többé nem kapunk kör alakú indukcióvonalakat. Érdemes lenne számítógépes szimulációval meghatározni az ellentétes irányú, de nem egyenlő nagyságú áramok keltette mágnestér indukcióvonalait, hiszen erre

r ≪ d

esetén (az egyik áram közvetlen közelében) ugyanúgy, mint

r ≫ d

esetén (ahonnan a két áram már egyetlen

| I_{1} - I_{2} |

nagyságú áramnak látszik) az indukcióvonalak egyre jobban hasonlítanak a körhöz. De milyen furcsa görbék jöhetnek ki közben?