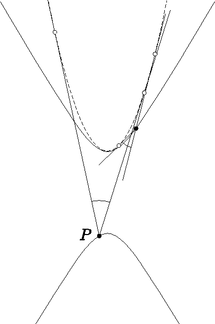Kezdőlap


Feladat:	B.3901	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Blázsik Zoltán , Bogár Péter , Csató László , Cseh Ágnes , Cserép Gergely , Csizmadija Laura , Dányi Zsolt , Farkas Ádám László , Fegyverneki Tamás , Gyöngyösi Zsolt , Honner Balázs , Károlyi Márton , Komáromy Dani , Kornis Bence , Kornis Kristóf , Kovács 129 Péter , Kovács Péter , Kozma Márton , Kunovszky Péter , Kutas Péter , Mészáros Gábor , Nagy János , Páldy Sándor , Pásztor Attila , Peregi Tamás , Szabó Tamás , Szakács Nóra , Szalkai Balázs , Szalóki Dávid , Szilágyi Csaba , Szűcs Gergely , Tomon István , Tossenberger Anna , Tóthmérész Lilla , Udvari Balázs , Varga László , Véges Márton
Füzet:	2007/január, 24 - 27. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Síkgeometriai számítások trigonometria nélkül, Egyenesek egyenlete, Mértani helyek, Feladat
Hivatkozás(ok):	Feladatok: 2006/március: B.3901

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Bármely két parabola hasonló, így az általánosság megszorítása nélkül föltehetjük, hogy a szóban forgó parabola egyenlete $y = x^{2}$ . Ekkor a fókusz koordinátái $F (0; \frac{1}{4})$ , a $v$ vezéregyenes egyenlete pedig $y = - \frac{1}{4}$ . Legyen $P (u; v)$ a parabola tetszőleges külső pontja; ismeretes, hogy ez pontosan akkor teljesül, ha $0 < u^{2} - v$ .
A $P$ -ből húzott érintők nem párhuzamosak a parabola tengelyével, így kereshetjük őket a $P$ -n átmenő $m$ meredekségű egyenesként, melynek egyenlete $y = m (x - u) + v$ . Ez az egyenes akkor és csak akkor érinti a parabolát, ha a görbével egyetlen közös pontja van, tehát az

\begin{matrix} y & = x^{2}, \\ y & = m (x - u) + v \end{matrix}

egyenletrendszernek egy megoldása van. Ez pontosan akkor teljesül, ha a behelyettesítéssel kapott

x^{2} - m x + m u - v = 0

másodfokú egyenlet diszkriminánsa,

\begin{matrix} m^{2} - 4 u m + 4 v = 0. \end{matrix}

(1)

Ennek az

m

-ben másodfokú egyenletnek a diszkriminánsa

16 u^{2} - 16 v

, ez külső pontra pozitív, az egyenlet két valós gyöke,

m_{1}

és

m_{2}

P

-ből húzható két érintő meredeksége. Ha

φ

jelöli a két érintő hajlásszögét, akkor a fenti jelölésekkel a

tg (α - β)

kifejtési képlete alapján:

\begin{matrix} | tg φ | = | \frac{m_{1} - m_{2}}{1 + m_{1} m_{2}} | . \end{matrix}

Mivel

tg 30^{\circ} = \frac{\sqrt[]{3}}{3}

, így azon

P

pontok halmazát keressük, amelyekre a fent kiszámolt

m_{1}

m_{2}

meredekségekkel

\begin{matrix} {(\frac{m_{1} - m_{2}}{1 + m_{1} m_{2}})}^{2} = \frac{1}{3} . \end{matrix}

(2)

A gyökök és együtthatók összefüggései szerint az (1) egyenletből

m_{1} + m_{2} = 4 u

és

m_{1} m_{2} = 4 v

. A (2) feltétel tehát az

(u; v)

számpárra azt jelenti, hogy

\begin{matrix} {(m_{1} + m_{2})}^{2} - 4 m_{1} m_{2} = 16 u^{2} - 16 v = \frac{1}{3} \cdot {(1 + m_{1} m_{2})}^{2} = \frac{1}{3} \cdot {(1 + 4 v)}^{2} . \end{matrix}

(3)

A keresett mértani hely egyenlete az

(u; v)

változókkal:

\begin{matrix} 48 (u^{2} - v) = {(1 + 4 v)}^{2} . \end{matrix}

Rendezés és teljes négyzetté alakítás után az egyenlet

\begin{matrix} u^{2} - \frac{{(v + \frac{7}{4})}^{2}}{3} = - 1 \end{matrix}

(4)

alakú. Ez egy, a kanonikus helyzethez képest eltolt és

90^{\circ}

-kal elforgatott hiperbola egyenlete (1. ábra). A hiperbola valós tengelye az

y

-tengely, képzetes tengelye az

x

-tengellyel párhuzamos

y = - \frac{7}{4}

egyenletű egyenes. A valós féltengely hossza

a = \sqrt[]{3}

, a képzetes féltengely hossza

b = 1

, így a fókuszoknak a centrumtól mért távolsága

\begin{matrix} c = \sqrt[]{a^{2} + b^{2}} = 2. \end{matrix}

A hiperbola fókuszai tehát

F_{1} (0; \frac{1}{4})

és

F_{2} (0; - \frac{15}{4})

1. ábra

Megjegyzések 1. A 2. ábrán látható, de a bizonyításból is kiolvasható, hogy a kapott hiperbola ,,alsó'' ágán azok a

P

pontok találhatók, amelyekből érintőket húzva a létrejövő

30^{\circ}

-os szögtartomány tartalmazza a parabolát, míg a ,,felső'' ág pontjaira a kiegészítő,

150^{\circ}

-os szögtartomány belsejében van a parabola.

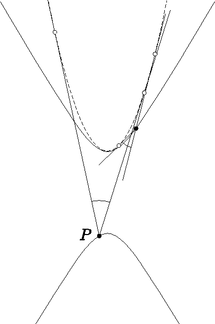2. ábra

2. Hasonló eredmény adódik, ha a feladatban adott

30^{\circ}

helyett tetszőleges hegyesszöget írunk elő. Ha az érintők szögét

90^{\circ}

-nak választjuk, akkor a mértani hely egyenlete a fentiek alapján az

m_{1} m_{2} = - 1

feltételből

4 v + 1 = 0

, ilyenkor a parabola vezéregyenesét kapjuk.
3. A válaszban felbukkant a parabola fókusza és ‐ speciális esetben ‐ a vezéregyenese is. Ha felhasználjuk a kúpszeletek ‐ és ezen belül a hiperbola ‐ egy kevésbé közismert származtatását, akkor ezek az eredmények egységes alakot öltenek. Hajós György: Bevezetés a geometriába című könyvének 422. oldalán olvasható a

42.5 Tétel. Azoknak a pontoknak a mértani helye, amelyekre egy ponttól való távolságukat egy a ponton át nem haladó egyenestől való távolságukkal osztva megadott pozitív értéket kapunk, ellipszis, hiperbola vagy parabola aszerint, amint az adott érték

1

-nél kisebb,

1

-nél nagyobb vagy

1

-gyel egyenlő. Ilyen mértani helyként minden kúpszeletet megkaphatunk.

Az adott pont a kúpszelet ‐ egyik ‐ fókusza, a rá nem illeszkedő egyenest általában is a kúpszelet vezéregyenesének nevezik, az adott állandót pedig a kúpszelet excentricitásának. A feladat megoldása ebben a formában közvetlenül is megkapható a (4) egyenletből: ha rendezés után mindkét oldalhoz

{(v + \frac{7}{4})}^{2} + 3 {(v - \frac{1}{4})}^{2}

-t adunk, (ez a lépés az eredmény ismerete nélkül nem egészen magától értetődő), akkor

\begin{matrix} 3 [u^{2} + {(v - \frac{1}{4})}^{2}] = 3 {(v - \frac{1}{4})}^{2} + {(v + \frac{7}{4})}^{2} - 3 = 4 v^{2} + 2 v + \frac{1}{4} = 4 {(v + \frac{1}{4})}^{2} \end{matrix}

adódik. A bal oldalon a

P

pontnak a parabola fókuszától való távolsága négyzetének a 3-szorosa, a jobb oldalon pedig a

P

vezéregyenestől való távolsága négyzetének a 4-szerese áll. Az idézett tétel szerint tehát a mértani hely egy olyan hiperbola, amelynek fókusza és vezéregyenese a parabola fókusza, illetve vezéregyenese. A tételben szereplő arány értéke

\frac{2}{\sqrt[]{3}}

. Akinek jó a számérzéke vagy egy kicsit tovább kísérletezik az (1) összefüggéssel, az eljuthat ennek az értéknek a jelentéséhez is. A most következő megoldásból, amely a parabola érintőinek geometriai tulajdonságait felhasználva közvetlenül a fenti tétel alapján talál rá a mértani helyre, ennek az aránynak az értéke is kiderül.

II. megoldás. Tegyük föl, hogy az

F

fókuszú

v

vezéregyenesű parabola a külsejében fekvő

P

pontból

α

szögben látszik. A fókusz tükörképét a két érintőre jelölje

G

és

H

; ezek a pontok, mint ismert, a vezéregyenesen vannak. Jelölje végül a

P

vetületét a vezéregyenesen

T

(3. ábra).

3. ábra

v

elválasztja

P

-t és

F

-et, akkor a tükrözések miatt

G P H ∢ = 2 α

, azért

G P T ∢ = α

. A

G P T

derékszögű háromszögben:

\begin{matrix} cos α = \frac{P T}{P G} = \frac{P T}{P F} . \end{matrix}

P

v

-nek ugyanarra az oldalára esik, mint

F

, akkor a 4. ábra szerint

\begin{matrix} G P T ∢ = 180^{\circ} - α . \end{matrix}

Ekkor a

G P T

derékszögű háromszögben:

\begin{matrix} - cos α = cos (180^{\circ} - α) = \frac{P T}{P G} = \frac{P T}{P F} . \end{matrix}

Mindez azt jelenti, hogy adott

α \neq 90^{\circ}

szög esetén a

\begin{matrix} | cos α | = \frac{P T}{P F} \end{matrix}

feltétel pontosan azokra a

P

pontokra teljesül, amelyekből a parabola

α

vagy

180^{\circ} - α

szögben látszik és a két lehetőség aszerint valósul meg, hogy hogy a parabola vezéregyenese elválasztja-e a

P

és az

F

pontokat vagy sem. Az idézett tétel szerint tehát a keresett mértani hely egy olyan hiperbola, amelynek a parabolával közös a fókusza és a vezéregyenese, excentricitása pedig

| cos α |

4. ábra

Megjegyzés. A fentiekből az is leolvasható, hogy

α = 90^{\circ}

esetén

P T = 0

, azaz ilyenkor a parabola vezéregyenesét kapjuk.