Kezdőlap


Feladat:	B.3857	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Cseh Ágnes , Dombi Soma , Dudás László , Faragó Kornél , Farkas Márton , Fegyverneki Tamás , Gyurcsik Judit , Hegyi Péter , Horváth Gábor , Kardos Kinga Gabriela , Károlyi Márton , Kovács Péter , Lamm Éva , Lovász László Miklós , Magda Gábor , Mészáros Gábor , Müller Márk , Nagy Gergely Gábor , Orosz Katalin , Quittner Bence , Szabó Tamás
Füzet:	2006/május, 292 - 293. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 2005/november: B.3857

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Ha a trapéz nem szimmetrikus, akkor egységnyi oldalú rombusz, amelynek a területe legfeljebb 1. Szimmetrikus trapéz esetében feltehető, hogy a negyedik oldal (a trapéz másik alapja) 1-nél nagyobb, hiszen ellenkező esetben a szárak ,,kifordításával'' egy nagyobb területű megfelelő trapézba foglalható (ld. az ábrán).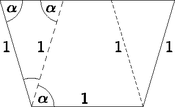

Használjuk az ábra jelöléseit: a száraknak az 1-nél nagyobb alappal bezárt szöge

α

. Bontsuk fel a trapézt egy egységnyi oldalú,

α

és

(180^{\circ} - α)

szögű rombuszra és egy egységnyi szárú egyenlő szárú háromszögre, amelynek a szárai

(180^{\circ} - 2 α)

szöget zárnak be egymással; nyilván

0 < α \leq 90^{\circ}

; az

α = 90^{\circ}

éppen az egységoldalú rombuszok körében maximális területű egységnégyzetnek felel meg. A trapéz területét az egyenlő szárú háromszög és a rombusz területének összegeként kaphatjuk:

\begin{matrix} T = \frac{1}{2} sin (180^{\circ} - 2 α) + sin α = \frac{1}{2} sin 2 α + sin α = sin α (cos α + 1) . \end{matrix}

Fejezzük ki mindezt

t = tg \frac{α}{2}

segítségével:

sin α = \frac{2 t}{1 + t^{2}}

cos α = \frac{1 - t^{2}}{1 + t^{2}}

, így

\begin{matrix} T = \frac{2 t}{1 + t^{2}} \cdot \frac{2}{1 + t^{2}} = \frac{4 t}{{(1 + t^{2})}^{2}} . \end{matrix}

α

-ra fennálló korlátok szerint

0 < \frac{α}{2} \leq 45^{\circ}

, ezért

0 < t \leq 1

. A számtani és a mértani közép közti egyenletlőtlenség miatt

\begin{matrix} 1 + t^{2} = \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + t^{2} \geq 4 \cdot \sqrt[4]{\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot t^{2}} = \frac{4 \cdot \sqrt[]{t}}{\sqrt[4]{27}}, \end{matrix}

ezért

\begin{matrix} T = \frac{4 t}{{(1 + t^{2})}^{2}} \leq \frac{4 t}{{(\frac{4 \cdot \sqrt[]{t}}{\sqrt[4]{27}})}^{2}} = \frac{4 t}{\frac{16 t}{\sqrt[]{27}}} = \frac{3 \sqrt[]{3}}{4} . \end{matrix}

Ezt a maximális értéket pontosan akkor veszi fel a terület, ha

\frac{1}{3} = t^{2}

, azaz

tg \frac{α}{2} = t = \frac{1}{\sqrt[]{3}} = tg 30^{\circ}

, vagyis ‐ mivel a tangensfüggvény kölcsönösen egyértelmű a

(0; 45^{\circ}]

intervallumon ‐ ha

α = 60^{\circ}