|
| Feladat: |
B.3636 |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Backhausz Ágnes , Bérczi Kristóf , Fehér Gábor , Füredi Mihály , Gehér György , Jankó Zsuzsanna , Jelitai Kálmán , Kiss-Tóth Christian , Korotij Ágnes , Kórus Péter , Mánfay Máté , Ruppert László Gábor , Salát Máté , Torma Róbert |
| Füzet: |
2005/április,
211 - 212. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Síkgeometriai szerkesztések, Konstruktív megoldási módszer, Feladat |
| Hivatkozás(ok): | Feladatok: 2003/április: B.3636 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Tekintsünk egy ilyen zárt töröttvonalat. Oldalain egy irányban haladva irányítsuk az oldalvektorokat. A töröttvonal zárt, ezért Rendezzük át az összeget úgy, hogy az egymásra merőleges vektorok szomszédosak legyenek, ezt megtehetjük a vektorok összeadásának kommutatív és asszociatív tulajdonsága miatt: Ez egyben azt is jelenti, hogy az , , vektorok hosszaira teljesül a háromszög-egyenlőtlenség. Így a töröttvonal létezésének szükséges feltétele, hogy a , , szakaszok közül egyik sem lehet nagyobb a másik kettő összegénél. Nem nehéz belátni e feltétel elégségességét is, hiszen ebből a három szakaszból egy legfeljebb elfajult háromszög szerkeszthető. Ezen háromszög megfelelő oldalaira kifelé megszerkesztjük a megfelelő derékszögű háromszögeket, a hosszú oldalra az és befogójú derékszögű háromszöget, és hasonlóan a többit. Már csak az oldalak átrendezésére van szükség, úgy, hogy szomszédos és , a és , valamint a és átellenesek legyenek. Ehhez az alábbi szomszédos oldalcserékre lesz szükség, amelyeket az 1. ábrán látható módon, esetenként elfajuló paralelogrammákkal valósíthatunk meg (a félkövérrel jelölt oldalakat cseréljük): | |
Nem zártuk ki azt a lehetőséget sem, hogy a töröttvonal szomszédos oldalai esetleg egy egyenesbe esnek.
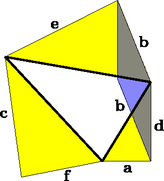 1. ábra
II. megoldás. Tegyük fel, hogy ilyen zárt töröttvonal, ahol , , , , , . Tükrözzük az pontot a szakasz felezőpontjára, az így kapott pontra és . Ezek az egymással egyenlő hosszúságú szakaszok egyben párhuzamosak is, tehát az szakasz merőleges a szakaszra, az szakasz pedig a szakaszra.
Ugyanígy tükrözve a pontot a oldal felezőpontjára, az pontot pedig a oldal felezőpontjára, olyan zárt töröttvonalhoz jutunk, melynek oldalai , , , , , , és az , , szakaszok rendre merőlegesek a , , szakaszokra. Az pontok tehát olyan, esetleg elfajuló háromszöget határoznak meg, melynek oldalai , , . Szükséges feltétel tehát, hogy ezen három szakasz közül egyik se legyen nagyobb a másik kettő összegénél.
Ez a feltétel egyben elégséges is. Ugyanis ha a , , szakaszokból megszerkesztjük az esetleg elfajuló háromszöget, majd ennek oldalaira a megfelelő , , derékszögű háromszögeket, ahol , , , , és (erre az általános esetben 8 különféle lehetőségünk van), akkor az , , pontokat rendre az , , szakaszok felezőpontjára tükrözve a feltételeknek megfelelő zárt töröttvonalat kapunk.
Bizonyításunk nem csak síkban adja meg a kívánt feltételt, példaként tekintsük a 2. ábrát.
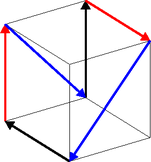 2. ábra |
|
 PDF |
PDF |  MathML
MathML 
