Kezdőlap


Feladat:	C.809	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	2006/február, 87 - 88. oldal		PDF \| MathML
Témakör(ök):	Kocka, Csonkagúlák, Térfogat, Pitagorasz-tétel alkalmazásai, C gyakorlat
Hivatkozás(ok):	Feladatok: 2005/április: C.809

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Illesszük a $K$ kocka még egy példányát, $K'$ -t az $A D H E$ laphoz az 1. ábra szerint. Az így adódó hasáb $M$ , $B$ , $G$ csúcsain átmenő sík nyilván áthalad a $P$ és az $R$ pontokon is, így azonos a metsző síkkal. Ez a sík a hasáb felületét az $M G, M B, B G$ lapátlókban metszi. A $K$ kockában ez a síkmetszet egy négyszög, amelynek $P$ és $Q$ csúcsai felezik az $M B$ és az $M G$ szakaszokat. A $P Q$ tehát középvonal az egyenlő szárú $M G B$ háromszögben, a $B P Q G$ síkmetszet tehát szimmetrikus trapéz. Nagyobbik alapja, $B G$ a kocka lapátlója, míg a másik, $P Q$ ennek fele. A szárak, $Q G$ és $P B$ közös hossza a hasáb $M G$ lapátlójának a fele.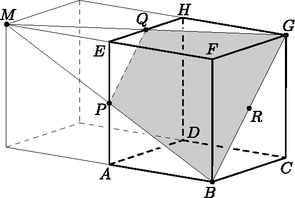

1. ábra

a)

A trapéz magassága fele az egyenlő szárú

M G B

háromszög

M R

magasságának. Pitagorasz tétele szerint

\begin{matrix} M R^{2} = M G^{2} - G R^{2} = M F^{2} + F G^{2} - G R^{2} = 4 + 1 - \frac{1}{2} = \frac{9}{2}, \end{matrix}

így a trapéz magassága

h = \frac{3 \sqrt[]{2}}{4}

. A trapéz területe

\begin{matrix} t = \frac{h}{2} (P Q + B G) = \frac{3 \sqrt[]{2}}{8} \cdot \frac{3 \sqrt[]{2}}{2} = \frac{9}{8} . \end{matrix}

Megjegyzések. 1. A síkmetszet szimmetrikus trapéz volta abból is következik, hogy a kocka és a metsző sík együttese szimmetrikus a kocka

E F C D

átlósíkjára.
2. Ha felhasználjuk a Pitagorasz-tételnek azt a térbeli kiterjesztését, amely szerint ha egy síkidomot három páronként merőleges síkra vetítünk, akkor a vetületek területének négyzetösszege a síkidom területének a négyzete, akkor gyorsabban célhoz érünk. A 2. ábrán a trapéz vetületei láthatók a kocka három lapján. A két egybevágó vetület területe a kockalap területének a

\frac{3}{4}

-e, a harmadik pedig ennek fele,

\frac{3}{8}

. A trapéz területének a négyzete így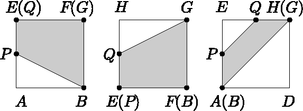

\begin{matrix} t^{2} = 2 \cdot {(\frac{3}{4})}^{2} + {(\frac{3}{8})}^{2} = \frac{9}{8} + \frac{9}{64} = \frac{81}{64}, \end{matrix}

ahonnan ismét az előző eredményt kapjuk.

2. ábra

b)

A metsző sík két testre vágja a

K

kockát. Egyikük egy csonkagúla, melynek fedőlapjai egyenlő szárú derékszögű háromszögek. A két kockából álló hasábban a

Q E P M

gúla a

G F B M

gúlává egészíti ki ezt a csonkagúlát. A két gúla középpontosan hasonló, a hasonlóság aránya

1 : 2

. A térfogatuk aránya így ennek a köbe,

1 : 8

, a

K

-beli csonkagúla térfogata tehát a

\frac{7}{8}

-a a

G F B M

gúla térfogatának, ami a kocka térfogatának a harmada. (

G F B

lapjának területe a kockalap fele, az ehhez tartozó

M F

magassága pedig a kockaél kétszerese.) A csonkagúla térfogata tehát a kocka térfogatának a

\frac{7}{24}

-e, így a részek térfogatának az aránya

7 : 17

Megjegyzés. Természetesen okoskodhattunk volna a csonkagúla ismert térfogatképlete szerint is.