Kezdőlap


Feladat:	3748. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Széchenyi Gábor , Tinku Szilárd
Füzet:	2005/május, 303 - 304. oldal		PDF \| MathML
Témakör(ök):	Kötelek (láncok) dinamikája, Feladat
Hivatkozás(ok):	Feladatok: 2004/november: 3748. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a kötélszárak hosszát $a$ -val és $b$ -vel, az általuk alkotott háromszögben a szemközti szögeket $α$ -val és $β$ -val (1. ábra). Az egyes kötélszárak tömege a kötél hosszával arányos:

\begin{matrix} m_{a} = \frac{a}{a + b} m, m_{b} = \frac{b}{a + b} m, \end{matrix}

ahol

m

az egész kötél tömege.

1. ábra

A kötélszárakat ‐ legalábbis az indulás pillanatában ‐ helyettesíthetjük egy-egy pontszerű testtel, melyeket egy csiga segítségével elhanyagolható tömegű fonál köt össze. A fonáldarab által kifejtett erőt

K

-val, az egyes darabok gyorsulását pedig (az ábrán látható irányítással)

A

-val jelölve a rendszer mozgásegyenlete:

\begin{matrix} m_{a} g sin β - K & = m_{a} A, \\ K - m_{b} g sin α & = m_{b} A, \end{matrix}

ahonnan a kötél gyorsulása:

\begin{matrix} A = \frac{m_{a} sin β - m_{b} sin α}{m_{a} + m_{b}} g = \frac{a sin β - b sin α}{a + b} g . \end{matrix}

Használjuk még ki, hogy bármely háromszögben az oldalak és a szögek között a szinusz-tételnek megfelelő kapcsolat áll fenn:

\begin{matrix} \frac{a}{b} = \frac{sin α}{sin β} . \end{matrix}

Innen

A = 0

következik, vagyis a kötél ‐ ha éppen a feladatban szereplő helyzetban hagyjuk magára ‐ egyik irányban sem kezd el mozogni, nyugalomban marad. (Belátható, hogy ez az egyensúlyi helyzet labilis.)

II. megoldás. Oldjuk meg a feladatot az ún. virtuális munka elvének segítségével, vagyis energetikai megfontolásokkal. Tegyük fel, hogy a kötelet egy kicsit (mondjuk

Δ l

távolságnyit) elmozdítjuk a jobb oldali kötélszár irányában. Ekkor a kötél gravitációs helyzeti energiája egy nagyon kicsit (

Δ l^{2}

-tel arányos mértékben) lecsökken, hiszen a helyzeti energia úgy számolható, mintha egy

Δ l

hosszúságú darabkát levágtunk volna a kötél bal oldali végéből, és azt a jobb oldali végponthoz ragasztottuk volna. Hasonló gondolatmenettel látható be, hogy a helyzeti energia akkor is csökkenne, ha a kötelet az ellenkező irányban mozdítanánk el.
Ezek szerint a kötél gravitációs helyzeti energiájának a feladat ábráján látható helyzetben maximuma van, ami pedig (egy domb tetején álló labda esetéhez hasonlóan) instabil egyensúlyi helyzetnek felel meg.
Elegánsabban is eljuthatunk a megoldáshoz, ha azt a módszert alkalmazzuk, amelyet Simon Stevin (1548‐1620) németalföldi tudós (neve latinosan Stevinus formában is ismert) fedezett fel, és amelyre utaló ábrát a sírkövére is felvésetett.
Tekintsünk egy apró szemekből álló gyöngysort (ez lényegében egyenértékű a hajlékony, homogén kötéllel), készítsünk belőle zárt láncot, majd helyezzük ezt a láncot egy kettős lejtőre (2. ábra). A lánc önmagától nem fordul körbe, nem gyorsul semelyik irányban; ha ilyet tenne, ,,örökmozgóvá'' válna.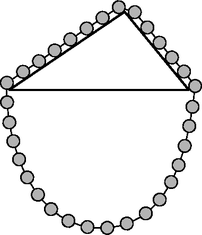

2. ábra

Világos, hogy a lánc alsó (szimmetrikus) része ‐ elfordulás szempontjából ‐ önmagában is egyensúlyban van, se jobbra, se balra nem akar elmozdulni. (Függőlegesen persze elmozdulna, ha a lánc többi része nem tartaná; ez azonban a megfontolásaink szempontjából lényegtelen.) Így tehát a lejtőn levő egyenes gyöngysor-szálak is egyensúlyban kell legyenek, az alsó rész eltávolítása után is nyugalomban maradnának.