Kezdőlap


Feladat:	3698. fizika feladat	Korcsoport: -	Nehézségi fok: nehéz
Megoldó(k):	Halász Gábor , Rakyta Péter
Füzet:	2005/január, 49 - 51. oldal		PDF \| MathML
Témakör(ök):	Merev test egyensúlya, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 2004/március: 3698. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A lyukas henger (mint merev test) egyensúlyának feltétele az, hogy a rá ható erők eredője is és a forgatónyomatékok eredője is nulla legyen. A hengerre ható külső erők eredője nyilván lehet nulla, hiszen a súrlódás elegendően nagy; probléma csak a forgatónyomatékokkal lehet.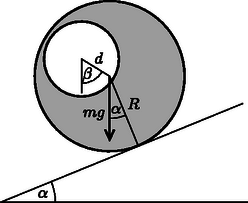
Ha a tömör henger tömege $m$ lenne, akkor a lyukas résznek megfelelő anyagmennyiség $m / 4$ tömegű. Tekintsük az 1. ábrán látható helyzetet, és írjuk fel a nehézségi erő forgatónyomatékát a henger és a lejtő érintkezési pontjára vonatkoztatva!

1. ábra

Egy tömör henger esetében a forgatónyomaték

\begin{matrix} m g R sin α \end{matrix}

lenne, de mivel a lyukas részben levő anyagmennyiség hiányzik, ennek forgatónyomatékát le kell vonni a fenti kifejezésből, s a maradék

\begin{matrix} M = m g R sin α - \frac{m}{4} g (R sin α + d sin β) . \end{matrix}

Megjegyzés. A fenti képlet úgy is értelmezhető, mintha a lyukas részre negatív (tehát függőlegesen felfelé mutató) gravitációs erő hatna, aminek forgatónyomatéka ellentétes a tömör hengerre ható forgatónyomatékkal.

Az eredő forgatónyomaték egyensúly esetében nulla kell legyen, ahonnan

\begin{matrix} sin α = \frac{d}{3 R} sin β \leq \frac{d}{3 R} . \end{matrix}

(1)

Az (1) egyenlőtlenség határesetében nem lehet biztos az egyensúly, hiszen csak egyetlen helyzetben,

β = 90^{\circ}

-nál teljesül

M = 0

. Ebből a helyzetből tetszőlegesen kicsit kimozdítva a lyukas hengert, az menthetetlenül legurul a lejtőn. Ha viszont határozottan az egyenlőtlenség teljesül, akkor biztos (stabil) egyensúly alakul ki, feltéve, hogy a lyukas rész a henger bal felső negyedébe esik. Képzeljük el ugyanis, hogy a lyukas hengert az egyensúlyi helyzetéből egy kicsit felfele gördítjük a lejtőn. Ekkor a ,,negatív gravitáció'' forgatónyomatéka lecsökken, tehát az eredő nyomaték az egyensúlyi helyzet felé forgatja vissza a rendszert; hasonló történik akkor is, ha az ellenkező irányba térítjük ki a hengert az egyensúlyából. Ugyanígy látható be, hogy ha a lyukas rész a henger bal alsó negyedében található, akkor az egyensúly bizonytalan (instabil).

II. megoldás. Számítsuk ki, hogy milyen messze van a lyukas henger tömegközéppontja a henger tengelyétől! Ha

s

-sel jelöljük ezt a távolságot és

\frac{3}{4} m

-mel a lyukas henger tömegét, akkor a lyukból hiányzó tömeg

\frac{1}{4} m

, és ha ezzel kiegészítjük a lyukas hengert, a tömegközéppont a szimmetriatengelyre kerül. Ennek feltétele:

\begin{matrix} \frac{3}{4} m \cdot s = \frac{1}{4} m \cdot d, \end{matrix}

ahonnan

s = d / 3

következik.
Induljunk ki a lyukas henger egy olyan helyzetéből, amikor a tömegközéppontja éppen a henger tengelye alatt helyezkedik el, és számítsuk ki, hogy mennyivel változik meg a gravitációs helyzeti energiája, ha a hengert a lejtőn lefelé csúszásmentesen gördítve

x

szöggel elforgatjuk. A 2. ábráról (amely az áttekinthetőség kedvéért nem méretarányos) leolvasható, hogy a henger

x R

szakasznyit mozdul el a lejtő mentén, a henger tengelye tehát

x R sin α

-val mélyebbre kerül, a tömegközéppontja viszont a henger tengelyéhez képest

s (1 - cos x)

távolságnyival megemelkedik. A rendszer teljes helyzeti energiája tehát (ha a kezdeti helyzetet tekintjük nulla energiájúnak)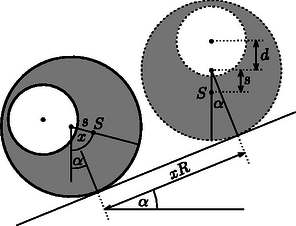

\begin{matrix} E (x) = \frac{3}{4} m g [- x R sin α + \frac{d}{3} (1 - cos x)] \end{matrix}

nagyságú lesz.

2. ábra

Biztos (stabil) egyensúlyi helyzet ott alakul ki, ahol az

E (x)

függvénynek lokális minimuma van; ennek feltétele pedig

E' (x) = 0

és

E'' (x) > 0

. Az előbbi a

\begin{matrix} - R sin α + \frac{d}{3} sin x = 0 \end{matrix}

(2)

egyenletre vezet, aminek

x

-re csak akkor van megoldása, ha

\begin{matrix} sin α \leq \frac{d}{3 R} . \end{matrix}

(3)

A második derivált akkor pozitív, ha

\begin{matrix} cos x > 0, \end{matrix}

(4)

emiatt (3)-ban az egyenlőség nem valósulhat meg, hiszen ekkor (2) szerint

sin x = 1

állna fenn, ez pedig ellentmondana (4)-nek.
A feladat megoldása tehát:

sin α < \frac{d}{3 R}