Kezdőlap


Feladat:	B.3668	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bednay Dezső , Bekényi Balázs , Bereczki Péter , Birkus Róbert , Bogár Péter , Csakurda Edit , Csizmadia János , Czank Tamás , Dudás János , Erdélyi Márton , Filus Tamás , Holló László , Hubai Tamás , Kaposi Ambrus , Kecskeméti Szabolcs , Kisfaludi-Bak Sándor , Kiss-Tóth Christián , Kórus Péter , Kovács Dóra Judit , Kunovszki Péter , Meszéna Balázs , Nagy Csaba , Nagy Péter , Nikházy László , Ozsvárt László , Pálinkás Csaba , Poronyi Balázs , Sándor Ágnes Petra , Sümegi Károly , Szabó Balázs , Szabó Tamás , Vaskó Richárd , Vass Márton , Vincze János , Üveges Lilla
Füzet:	2005/január, 28 - 30. oldal		PDF \| MathML
Témakör(ök):	Abszolútértékes egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2003/október: B.3668

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elegendő megvizsgálnunk, hogy hol van olyan $x_{0}$ , amelyre az $x \in [x_{0}; x_{0} + 1]$ intervallumban az $x \mapsto x^{2}$ függvény legnagyobb és legkisebb értéke közti különbség legfeljebb $\frac{1}{4}$ . Ha ugyanis egy ilyen $x_{0}$ -ra a függvény grafikonját az $x$ -tengellyel párhuzamosan eltoljuk úgy, hogy az $x_{0}$ a 0-ba, majd az $y$ -tengellyel párhuzamosan eltoljuk úgy, hogy a minimum értéke a $- \frac{1}{8}$ -ba kerüljön, akkor a kapott $x \mapsto x^{2} - a x - b$ függvényre teljesül a feladat előírása.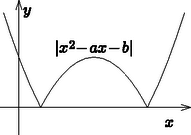

Megfordítva, minden megfelelő

a

és

b

számra az

x \mapsto x^{2} - a x - b

függvényre alkalmas lineáris transzformációt alkalmazva az

x \mapsto x^{2}

függvényhez jutunk, amely valamilyen

[x_{0}; x_{0} + 1]

intervallumon legfeljebb

\frac{1}{4}

-et változik. Keressünk tehát az

x \mapsto x^{2}

függvényhez ilyen

x_{0}

értékeket. Az egyszerűség kedvéért jelölje az

x \mapsto x^{2}

függvény maximumát és minimumát az

[x_{0}; x_{0} + 1]

intervallumon

M_{x_{0}}

és

m_{x_{0}}

. Az

x_{0}

lehetséges értékei szerint több esetet különböztetünk meg.
1. eset:

x_{0} \geq 0

. Ekkor a függvény az

[x_{0}; x_{0} + 1]

intervallumban szigorúan monoton növekvő, a minimumát

x_{0}

-ban, a maximumát

(x_{0} + 1)

-ben veszi föl.

\begin{matrix} M_{x_{0}} - m_{x_{0}} = {(x_{0} + 1)}^{2} - x_{0}^{2} = 2 x_{0} + 1 \geq 1. \end{matrix}

2. eset:

x_{0} \leq - 1

. Ekkor a függvény az

[x_{0}; x_{0} + 1]

intervallumban szigorúan monoton csökkenő, a maximumát

x_{0}

-ban, a minimumát

(x_{0} + 1)

-ben veszi föl.

\begin{matrix} M_{x_{0}} - m_{x_{0}} = x_{0}^{2} - {(x_{0} + 1)}^{2} = - 2 x_{0} - 1 \geq 1. \end{matrix}

3. eset:

- 1 < x_{0} \leq - \frac{1}{2}

. Ekkor

| x_{0} | \geq x_{0} + 1

, tehát

M_{x_{0}} = x_{0}^{2}

és

m_{x_{0}} = 0

, így

M_{x_{0}} - m_{x_{0}} \leq \frac{1}{4}

akkor és csak akkor teljesül, ha

| x_{0} | \leq \frac{1}{2}

, ami a megadott intervallumon csak az

x_{0} = - \frac{1}{2}

esetben lehetséges.
4. eset:

- \frac{1}{2} < x_{0} \leq 0

. Ekkor

| x_{0} | < x_{0} + 1

, tehát

M_{x_{0}} = {(x_{0} + 1)}^{2}

és

m_{x_{0}} = 0

. Most

M_{x_{0}} - m_{x_{0}} \leq \frac{1}{4}

akkor és csak akkor teljesül, ha

| x_{0} + 1 | \leq \frac{1}{2}

, ami most nem lehetséges, hiszen

x_{0} + 1 > \frac{1}{2}

.
Tehát

x_{0} = - \frac{1}{2}

az egyetlen olyan érték, hogy az

x \mapsto x^{2}

függvény megváltozása az

[x_{0}; x_{0} + 1]

intervallumon legfeljebb

\frac{1}{4}

‐ és ezen az intervallumon éppen ennyi. Így tehát mind az

x

-, mind az

y

-tengellyel párhuzamos eltolás egyértelműen meghatározott:

\begin{matrix} f (x) = {(x - \frac{1}{2})}^{2} - \frac{1}{8} = x^{2} - x + \frac{1}{8} . \end{matrix}

Így a megadott feltétel egyedül az

a = 1

és a

b = - \frac{1}{8}

esetben teljesül.

II. megoldás. Vezessük be az

f (x) = x^{2} - a x - b

függvényt. A feladat feltétele ekkor

| f (x) | \leq \frac{1}{8}

, ha

0 \leq x \leq 1

. A megoldásból kiderül, hogy az

f

függvényt már három alkalmas helyettesítési érték,

f (0)

f (\frac{1}{2})

és

f (1)

meghatározza.

\begin{matrix} f (0) = - b; f (\frac{1}{2}) = \frac{1}{4} - \frac{a}{2} - b; f (1) = 1 - a - b . \end{matrix}

(1)

| f (0) | \leq \frac{1}{8}

akkor és csak akkor teljesül, ha

- \frac{1}{8} \leq b \leq \frac{1}{8}

.
(2)

| f (\frac{1}{2}) | \leq \frac{1}{8}

akkor és csak akkor teljesül, ha

\frac{1}{8} \leq \frac{a}{2} + b \leq \frac{3}{8}

.
(3)

| f (1) | \leq \frac{1}{8}

akkor és csak akkor teljesül, ha

\frac{7}{8} \leq a + b \leq \frac{9}{8}

.
Ábrázoljuk a három egyenlőtlenség megoldáshalmazát egy derékszögű koordinátarendszerben.
Az ábráról leolvasható, hogy a (2) és (3) egyenlőtlenség megoldáshalmazát a

P Q R S

paralelogramma szemlélteti. A

P

csúcs koordinátái

P (1; - \frac{1}{8})

, a paralelogramma többi része pedig az

y = - \frac{1}{8}

egyenes alatt van. Így a

P

pont az egyetlen, amelynek koordinátáira mindhárom egyenlőtlenség teljesül, ha van a feladatnak megoldása, akkor csak

a = 1

b = - \frac{1}{8}

lehetséges.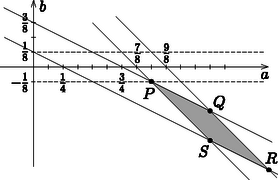

Az pedig ‐ például teljes négyzetté alakítva ‐ nyomban adódik, hogy az

f (x) = x^{2} - x + \frac{1}{8}

függvényre teljesül a feladat előírása. Valóban:

f (x) = {(x - \frac{1}{2})}^{2} - \frac{1}{8}

és ha

0 \leq x \leq 1

, akkor

| x - \frac{1}{2} | \leq \frac{1}{2}

, tehát

\begin{matrix} - \frac{1}{8} \leq f (x) \leq \frac{1}{4} - \frac{1}{8} = \frac{1}{8} . \end{matrix}

Megjegyzések. 1. Könnyű meggondolni, hogy az

a = 1

b = - \frac{1}{8}

értékeket már az

f (0) \geq - \frac{1}{8}

;

f (\frac{1}{2}) \geq - \frac{1}{8}

;

f (1) \leq \frac{1}{8}

feltételek is meghatározzák.
2. Igen gyorsan célhoz érünk, ha észrevesszük, hogy

\begin{matrix} \frac{f (0) + f (1)}{2} = \frac{1}{2} - \frac{a}{2} - b = \frac{1}{4} + f (\frac{1}{2}), \end{matrix}

ahonnan ‐ felhasználva a feltételt ‐ kapjuk, hogy

\begin{matrix} 0 \leq \frac{1}{8} + f (\frac{1}{2}) = \frac{f (0) - \frac{1}{8} + f (1) - \frac{1}{8}}{2} \leq 0, \end{matrix}

tehát csak

f (\frac{1}{2}) = - \frac{1}{8}

és

f (0) = f (1) = \frac{1}{8}

lehetséges. Ezek az értékek a másodfokú polinomot egyértelműen meghatározzák.