Feladat:	B.3742	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Blázsik Zoltán ,  Bozi Áron ,  Cseh Ágnes ,  Cserép Gergely ,  Csóka Győző ,  Dudás János ,  Eisenberger András ,  Farkas Ádám László ,  Grósz Dániel ,  Horváth Eszter ,  Juhász Gergely ,  Károlyi Gergely ,  Kiss Viktor ,  Kiss-Tóth Christián ,  Knippl Diána ,  Kovács Péter ,  Kovács Zoltán ,  Mátyás Péter ,  Mészáros Gábor ,  Muntag Lőrinc ,  Nagy Péter ,  Nagy-Baló András ,  Németh Attila György ,  Regős Gábor ,  Strenner Balázs ,  Szabó Tamás ,  Szalkai Balázs ,  Szilágyi Áron ,  Tardos Zsófia ,  Tóth Balázs ,  Udvari Balázs ,  Ureczky Bálint ,  Vásárhelyi Bálint Márk ,  Wojuteczky Péter
Füzet:	2005/május, 277 - 278. oldal		PDF  |  MathML
Témakör(ök):	Logikai feladatok, Feladat
Hivatkozás(ok):	Feladatok: 2004/szeptember: B.3742

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Először belátjuk, hogy az 1. állításból következik a 2., 3., 4. állítás. Legyen $n$ égimeszelő és $m$ kockafejű $\left(m\mathrm{,}n>0\right)$. $1\to 2$, mert $m>0$. (Feltettük, hogy az 1. teljesül.) $1\to 3$, mert $n>0$. (Feltettük, hogy az 1. teljesül.) $1\to 4$, mert az értékek átlaga a legalacsonyabb és a legmagasabb érték közé esik. A legalacsonyabb égimeszelő magasabb a legmagasabb kockafejűnél, az 1. teljesülése esetén. Ezek után lássunk néhány példát az osztály lehetséges összetételéről: 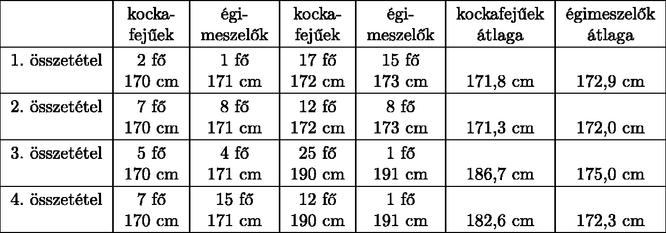    A 2. állításból nem következik az 1. állítás. Ellenpélda lehet az 1. összetétel, mert $2>1$, de egy égimeszelő nem magasabb minden kockafejűnél. A 2. állításból nem következik a 3. állítás. Ellenpélda lehet az 1. összetétel, mert $2>1$, de 16 nem nagyobb, mint 17. A 2. állításból nem következik a 4. állítás. Ellenpélda lehet a 3. összetétel, mert $5>4$, de 175,0 nem nagyobb, mint 186,7. A 3. állításból nem következik az 1. állítás. Ellenpélda lehet a 2. összetétel, mert $16>12$, de van olyan égimeszelő, akinél van magasabb kockafejű. A 3. állításból nem következik a 2. állítás. Ellenpélda lehet a 2. összetétel, mert $16>12$, de 7 nem nagyobb, mint 8. A 3. állításból nem következik a 4. állítás. Ellenpélda lehet a 4. összetétel, mert $16>12$, de 172,3 nem nagyobb, mint 182,6. A 4. állításból nem következik az 1. állítás. Ellenpélda lehet az 1. összetétel, mert $172\mathrm{,}9>171\mathrm{,}8$, de van olyan égimeszelő, akinél van magasabb kockafejű. A 4. állításból nem következik a 2. állítás. Ellenpélda lehet a 2. összetétel, mert $172\mathrm{,}0>171\mathrm{,}3$, de 7 nem nagyobb, mint 8. A 4. állításból nem következik a 3. állítás. Ellenpélda lehet az 1. összetétel, mert $172\mathrm{,}9>171\mathrm{,}8$, de 16 nem nagyobb, mint 17. A feladat kérdésére válaszunkat a következő táblázatban foglaljuk össze: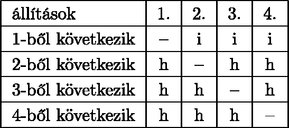