Kezdőlap


Feladat:	A.323	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Agócs István , Birkner Tamás , Birkus Róbert , Chelnokov Volodymyr , Czank Tamás , Dobos Gábor , Dobrovolska Galyna , Egri Attila , Estélyi István , Farkas Balázs , Gáti Beatrix , Hablicsek Márton , Horváth Márton , Hubai Tamás , Király Csaba , Kiss Domonkos , Kiss-Tóth Christián , Kocsis Albert Tihamér , Kórus Péter , Maga Péter , Magonyi Erika , Mánfay Máté , Mészáros Tamás , Németh Adrián , Pach Péter Pál , Paulin Roland , Pongrácz András , Puskás Anna , Rácz Béla András , Richter Péter , Sali András , Seres Gyula , Torma Róbert
Füzet:	2004/április, 230 - 231. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Euler-egyenes, Nehéz feladat
Hivatkozás(ok):	Feladatok: 2003/szeptember: A.323

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy mindhárom Euler-egyenes átmegy az $A B C$ háromszög súlypontján. Elég ezt a $B C I$ háromszög Euler-egyenesére igazolni, mivel egyik csúcsnak sincs kitüntetett szerepe.

1. ábra

Rajzoljunk a

B C

oldalra kifelé egy szabályos háromszöget, ennek harmadik csúcsa legyen

A'

, középpontja

O_{1}

. Az

I B A' C

négyszög húrnégyszög, mert

B A' C ∢ + C I B ∢ = 60^{\circ} + 120^{\circ} = 180^{\circ}

. Mivel

A' B = A' C

, az

A' I

szakasz felezi a

C I B

szöget. Ebből következik, hogy

A

I

és

A'

egy egyenesen van (1. ábra).
Legyen a

B C

szakasz felezőponta

F

, az

A B C

háromszög súlypontja

S

, a

B C I

háromszög súlypontja

S_{1}

. Mivel

S

S_{1}

és

O_{1}

nem más, mint az

A F

I F

, illetve

A' F

szakaszok

F

-hez közelebbi harmadolópontja, az

S

S_{1}

és

O_{1}

pontok is egy egyenesen vannak. Tehát, a

B C I

háromszög Euler egyenese,

O_{1} S_{1}

átmegy az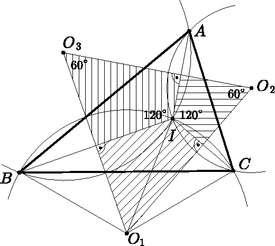

S

ponton.

II. megoldás. Legyen a

B C I

C A I

A B I

háromszögek körülírt körének középpontja rendre

O_{1}

O_{2}

O_{3}

, magasságpontjaik

M_{1}

M_{2}

, illetve

M_{3}

. Az

O_{1} O_{2}

O_{2} O_{3}

O_{3} O_{1}

egyenesek éppen a

C I

A I

, illetve

B I

szakaszok felező merőlegesei, és a bevonalkázott négyszögek szögeinek összeszámolásából kapjuk, hogy az

O_{1} O_{2} O_{3}

háromszög mindegyik szöge

60^{\circ}

, az

O_{1} O_{2} O_{3}

háromszög szabályos (2. ábra).

2. ábra

Megmutatjuk, hogy az

A B I

B C I

és

C A I

háromszögek Euler-egyenesei rendre átmennek az

O_{1} O_{2} O_{3}

háromszög középpontján. Elég ezt az egyik háromszögre igazolni; vizsgáljuk tehát a

B C I

háromszöget. Mivel

B O_{1} ó I O_{1} = C O_{1}

, az

O_{1} O_{2}

és

O_{1} O_{3}

egyenesek szögfelezők a

I O_{1} C

és

B O_{1} I

szögekben, azért

B O_{1} C ∢ = 2 O_{3} O_{1} O_{2} ∢ = 2 \cdot 60^{\circ} = 120^{\circ}

(3. ábra).

3. ábra

Jelöljük a

B I

és

C M_{1}

egyenesek metszéspontját

U

-val,

C I

és

B M_{1}

metszéspontját

V

-vel. Az

M_{1} V I U

négyszög szögeinek összeszámolásából

C M_{1} B ∢ = 60^{\circ}

. Az

M_{1} B O_{1} C

négyszög húrnégyszög, mert

C M_{1} B ∢ + B O_{1} C ∢ = 60^{\circ} + 120^{\circ} = 180^{\circ}

. Mivel pedig

B O_{1} = O_{1} C

, az is igaz, hogy

C M_{1} O_{1} ∢ = O_{1} M_{1} B ∢ = 30^{\circ}

.
Végül, az

M_{1} O_{1} O_{2}

és

O_{1} M_{1} B

szögek, valamint az

O_{3} O_{1} M_{1}

és

C M_{1} O_{1}

szögek váltószögek, ezért

M_{1} O_{1} O_{2} ∢ = O_{3} O_{1} M_{1} ∢ = 30^{\circ}

. A

B C I

háromszög Euler-egyenese,

O_{1} M_{1}

tehát nem más, mint az

O_{3} O_{1} O_{2}

szög felezője, átmegy tehát az

O_{1} O_{2} O_{3}

háromszög középpontján.