Kezdőlap


Feladat:	B.3717	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Filus Tamás
Füzet:	2004/december, 543 - 544. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Hossz, kerület, Terület, felszín, Téglalapok, Feladat
Hivatkozás(ok):	Feladatok: 2004/március: B.3717

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A $H$ téglalap oldalait jelöljük $a$ , $b$ -vel, a $H_{1}$ téglalapét pedig $c$ , $d$ -vel. Tudjuk, hogy $T_{H} = a b = 1$ , $K_{H} = 2 (a + b)$ , $T_{H_{1}} = c d = 1, 5$ (50%-kal nagyobb, mint $H$ területe) és $K_{H_{1}} = 2 (c + d) = a + b$ (50%-kal kisebb, mint $H$ kerülete). $K_{H} = 2 (a + b) = 4 (c + d)$ minimumát keressük ezen feltételek mellett. Az $a$ , $b$ , $c$ , $d$ értékek szakaszok hosszai, ezért mind pozitívak. Így oszthatunk $d$ -vel: $c = \frac{1, 5}{d}$ , és ezt a korábbi összefüggésekkel egybevetve $K_{H} = 4 (c + d) = \frac{6}{d} + 4 d$ adódik. A számtani és mértani közepek közötti egyenlőtlenség segítségével becsülhetjük $K_{H}$ -t, ugyanis tudjuk, hogy

\begin{matrix} \frac{6}{d} + 4 d \geq 2 \cdot \sqrt[]{\frac{6}{d} \cdot 4 d}, azaz \frac{6}{d} + 4 d \geq 4 \sqrt[]{6}, \end{matrix}

és egyenlőség pontosan akkor áll fenn, ha

\frac{6}{d} = 4 d

teljesül. Tehát

H

kerülete legalább

4 \sqrt[]{6}

. Belátjuk, hogy ez a becslés éles, azaz létezik olyan

H

téglalap, melynek ennyi a kerülete és a többi feltételnek is megfelel.
Láttuk, hogy csak akkor lehet egyenlőség, ha

\frac{6}{d} = 4 d

, azaz

4 d^{2} = 6

. Mivel

d

pozitív, azért

d = \frac{\sqrt[]{6}}{2}

, ebből pedig

c = \frac{1, 5}{d} = \frac{\sqrt[]{6}}{2}

. A

H_{1}

téglalap tehát négyzet, oldala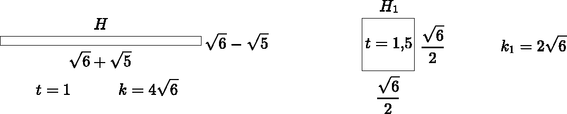

\frac{\sqrt[]{6}}{2}

H

oldalai,

a

és

b

egymás reciprokai. Ha a

H

kerülete

4 \sqrt[]{6}

, azaz

2 (\frac{1}{b} + b) = 4 \sqrt[]{6}

, akkor

2 (1 + b^{2}) = 4 \sqrt[]{6} b

, ahonnan rendezés után a

2 b^{2} - 4 \sqrt[]{6} b + 2 = 0

másodfokú egyenlet adódik, melynek gyökei:

\begin{matrix} b_{1,2} = \frac{4 \sqrt[]{6} \pm \sqrt[]{96 - 16}}{4} = \sqrt[]{6} \pm \sqrt[]{5} . \end{matrix}

A gyökök szorzata az ismert azonosság alapján

6 - 5 = 1

, vagyis a két gyök ugyanazt a téglalapot határozza meg. A feltételeknek megfelelő minimális kerületű

H

téglalap oldalai tehát

\sqrt[]{6} + \sqrt[]{5}

és

\sqrt[]{6} - \sqrt[]{5}

Megjegyzés. A számtani és mértani közepek közötti egyenlőtlenség közvetlen felhasználása helyett néhányan egy ismert eredményre hivatkoztak: az egyik téglalap kerülete a másik fele, így a kerületük ugyanakkor lesz minimális. Ezzel a feladatot arra vezethetjük vissza, hogy adott területű téglalapok közül melyiknek minimális a kerülete. Ez a négyzet (a fenti megoldásból is kiderül, hogy a

H_{1}

téglalap négyzet), mint az a számtani és mértani közepek közötti egyenlőtlenségből bizonyítható. Mások például egy-egy másodfokú egyenlet diszkriminánsának vizsgálatával jutottak a helyes eredményhez.