Kezdőlap


Feladat:	B.3694	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Nagy Csaba
Füzet:	2004/október, 413 - 415. oldal		PDF \| MathML
Témakör(ök):	Háromszög területe, Síkgeometriai szerkesztések, Konvex négyszögek, Feladat
Hivatkozás(ok):	Feladatok: 2004/január: B.3694

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen $P$ a négyszög $B D$ átlójának tetszőleges belső pontja. Ekkor az $A P C$ töröttvonal ugyanolyan arányban osztja az $A B C D$ négyszög területét, amilyen arányban $P$ osztja a $B D$ átlót, hiszen az $A P B$ és az $A P D$ háromszögek $A$ -hoz tartozó magassága is, és a $C P B$ és a $C P D$ háromszögek $C$ -hoz tartozó magassága is közös, tehát

\begin{matrix} \frac{T_{A P B}}{T_{A P D}} = \frac{P B}{P D} és \frac{T_{C P B}}{T_{C P D}} = \frac{P B}{P D}, \end{matrix}

vagyis

\begin{matrix} \frac{T_{A P C B}}{T_{A P C D}} = \frac{P B}{P D} . \end{matrix}

Ha a

P

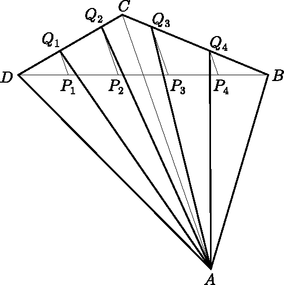
-n átmenő, az

A C

átlóval párhuzamos egyenes a

B C D

töröttvonalat a

Q

pontban metszi (a szimmetria miatt feltehetjük, hogy

Q

C D

oldalon van), akkor az

A P C

és az

A Q C

háromszögek területe megegyezik, mert

A C

oldaluk közös, az ehhez tartozó magasságaik pedig egyenlőek

P Q

és

A C

párhuzamossága miatt. Ezért

T_{A P C D} = T_{A Q D}

, vagyis

\begin{matrix} \frac{T_{A P C B}}{T_{A Q D}} = \frac{P B}{P D} . \end{matrix}

Ha tehát

P

B D

átló

D

-hez legközelebbi ötödölőpontja, akkor az

A Q

egyenes a négyszög területének ötödét vágja le.

1. ábra

Ezek alapján a szerkesztés menete:

‐	A $B D$ átlót öt egyenlő részre osztjuk (pl. a párhuzamos szelők tételén alapuló szerkesztéssel), az így kapott osztópontok $P_{1}$ , $P_{2}$ , $P_{3}$ és $P_{4}$ .

‐	A $P_{i}$ $(i = 1,2,3,4)$ pontokon át párhuzamosokat húzunk az $A C$ átlóval, ezeknek és a $B C D$ töröttvonalnak a metszéspontjait $Q_{i}$ -vel jelöljük.

‐	Összekötjük $A$ -t a $Q_{i}$ pontokkal (2. ábra).

2. ábra

Az előzőekben leírtakból következik, hogy az

A Q_{i}

egyenesek öt egyenlő területű részre osztják az

A B C D

négyszöget. A szerkesztés a négyszög konvexsége miatt mindig elvégezhető, a feladatnak minden esetben pontosan egy megoldása van.