Kezdőlap


Feladat:	3661. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hagymási Imre , Horváth Márton
Füzet:	2004/május, 306 - 307. oldal		PDF \| MathML
Témakör(ök):	Gauss-törvény, Feladat
Hivatkozás(ok):	Feladatok: 2003/november: 3661. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Osszuk fel gondolatban a lemezt sok kicsiny, egyenként $a$ nagyságú felületdarabkára! Mivel a lemez töltése egyenletes, a felületi töltéssűrűsége (egységnyi felületre jutó töltése) mindenütt $σ = \frac{Q}{d^{2}}$ , a vizsgált lemezdarabka töltése pedig $σ a$ . A Coulomb-törvény szerint a lemezdarabka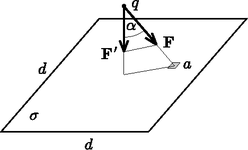

\begin{matrix} F = \frac{1}{4 π ε_{0}} \cdot \frac{q σ a}{r^{2}} \end{matrix}

nagyságú erőt fejt ki a ponttöltésre (

r

a felületdarabka és a ponttöltés távolsága). A rendszer szimmetriájából adódóan a ponttöltésre ható erő a lemezre merőleges kell legyen, az

F

erőnek tehát csak a felületre merőleges

\begin{matrix} F' = \frac{1}{4 π ε_{0}} \cdot \frac{q σ a}{r^{2}} \cdot cos α \end{matrix}

komponense játszik szerepet az eredő erő kiszámításánál (1. ábra).

1. ábra

Vizsgáljuk meg ezek után a ponttöltés elektromos terének a kérdéses felületdarabkán áthaladó fluxusát! A térerősség nagysága a felületdarabka helyén

\begin{matrix} E = \frac{1}{4 π ε_{0}} \cdot \frac{q}{r^{2}}, \end{matrix}

a fluxus tehát

\begin{matrix} Ψ = E \cdot a \cdot sin β, \end{matrix}

ahol

β

az elektromos térerősség és a felület síkja által bezárt szög (2. ábra). Mivel

β = 90^{\circ} - α

, a fluxus így is felírható:

\begin{matrix} Ψ = \frac{1}{4 π ε_{0}} \cdot \frac{q a}{r^{2}} \cdot cos α . \end{matrix}

2. ábra

Vegyük észre, hogy a felületdarabka által kifejtett

F'

erő arányos a vizsgált felületdarabkán áthaladó elektromos fluxussal:

F' = σ \cdot Ψ

, és ugyanez a kapcsolat a ponttöltésre ható eredő erő és a négyzetlapon áthaladó teljes elektromos fluxus között is:

F_{eredő} = σ \cdot Ψ_{négyzet}

.
Hogyan határozhatjuk meg a négyzetlapon áthaladó elektromos fluxust? Használjuk ki, hogy a ponttöltés

d / 2

távol van a lemeztől, vagyis éppen egy olyan kocka középpontjában, amelynek egyik lapja a négyzet alakú szigetelő lemez (3. ábra). Gauss törvénye szerint egy

q

töltésű pontszerű testből kiinduló teljes fluxus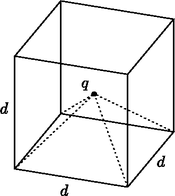

\begin{matrix} Ψ_{teljes} = \frac{q}{ε_{0}}, \end{matrix}

és ez a fluxus ‐ a szimmetria miatt ‐ egyenletesen oszlik meg a kocka 6 lapja között:

\begin{matrix} Ψ_{négyzet} = \frac{1}{6} \cdot Ψ_{teljes} = \frac{q}{6 ε_{0}}, \end{matrix}

a ponttöltésre ható erő tehát

\begin{matrix} F_{eredő} = \frac{σ q}{6 ε_{0}} = \frac{1}{6 ε_{0}} \cdot \frac{q Q}{d^{2}} . \end{matrix}

3. ábra

Megjegyzés. Integrálszámítás segítségével a lemezre merőleges szimmetriatengely tetszőleges pontjában kiszámítható a ponttöltésre ható erő. Ha a

q

töltésű test

x

távolságban van a lemeztől, akkor rá

\begin{matrix} F (x) = \frac{q Q}{π ε_{0} d^{2}} \cdot [arctg (\frac{d}{2 x}) - arctg (\frac{2 x d}{d^{2} + 4 x^{2} + d \sqrt[]{2 d^{2} + 4 x^{2}}})] \end{matrix}

erő hat.
Három határesetben is tanulságos a fenti kifejezés vizsgálata:

a)

x ≪ d

, akkor a szögletes zárójelben álló kifejezés

π / 2

-höz tart, ilyenkor

F = \frac{q Q}{2 ε_{0} d^{2}}

. Ez egy nagyméretű síkkondenzátor belsejében levő ponttöltésre ható erő esetének felel meg.

b)

x ≫ d

, akkor a szögletes zárójelben álló kifejezés

{(2 d / x)}^{2}

-tel közelíthető, az erőhatás pedig két pontszerűnek tekinthető töltés közötti Coulomb-erő képletével számítható.

c)

Végül tekintsük a feladatban szereplő

x = d / 2

esetet! A szögletes zárójelben szereplő kifejezés ekkor

\begin{matrix} arctg 1 - arctg (2 - \sqrt[]{3}) = \frac{π}{4} - \frac{π}{12} = \frac{π}{6}, \end{matrix}

az erő tehát az elemi úton is megkapható

\frac{q Q}{6 ε_{0} d^{2}}

-tel egyezik meg.