Kezdőlap


Feladat:	B.3628	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csajbók Bence , Pongrácz András , Salát Máté
Füzet:	2004/február, 90 - 92. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Négyszögek geometriája, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 2003/március: B.3628

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A négyszög csúcsait jelölje $A$ , $B$ , $C$ és $D$ , az oldalfelező pontokat pedig $E$ , $F$ , $G$ és $H$ az 1. ábra szerint. A két középvonal $M$ metszéspontját az oldalfelező pontokkal összekötő szakaszok súlyvonalak abban a négy háromszögben, amelyekre az $M$ -et a csúcsokkal összekötő szakaszok osztják a négyszöget. Ezek a szakaszok tehát rendre felezik az egyes háromszögek területét. Ebből következik, hogy

\begin{matrix} [E A F M] + [H M G C] = [D E M H] + [M F B G] = \frac{t}{2}, \end{matrix}

(1)

ahol

t

A B C D

négyszög területe. (

[E A F M]

annak a négyszögnek a területét jelöli, amelynek csúcsai

E

A

F

és

M

, a további tagok jelentése hasonló.) Ez következik abból, hogy mind a négy pár egyenlő területű háromszög egyike a fenti összeg bal, a másika pedig a jobb oldalán szerepel.

1. ábra

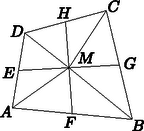Válasszuk az egyszerűség kedvéért a területmérés egységének a 180 m

^{2}

-t. Ekkor az ismert területű négyszögek rendre 2, 4 és 5 egység területűek. Az (1) egyenlőség szerint három eset lehetséges attól függően, hogy az ismeretlen területű negyedik rész melyik ismert területű kis négyszöggel van ,,átlósan'' szemközt a három közül. Ezek az esetek láthatók a 2/a., b., c. ábrákon. Megmutatjuk, hogy közülük kettő nem jöhet létre.

\begin{matrix} \begin{matrix} t = 12, \frac{t}{8} = \frac{3}{2} > 1 2/a. ábra \end{matrix}\begin{matrix} t = 14, \frac{t}{8} = \frac{7}{4} 2/b. ábra \end{matrix}\begin{matrix} t = 18, \frac{t}{8} = \frac{9}{4} > 2 2/c. ábra \end{matrix} \end{matrix}

Ismeretes, hogy egy négyszög oldalfelező pontjai paralelogrammát határoznak meg, melynek területe fele a négyszögének. Az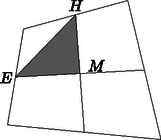

A B C D

négyszög középvonalai átlók ebben az

E F G H

paralelogrammában, azt tehát négy egyenlő,

\frac{t}{8}

területű háromszögre osztják. E háromszögek közül mind a négy örökrész tartalmaz egyet, azért mindegyikük területe nagyobb, mint

\frac{t}{8}

(3. ábra). Ez pedig egyedül a második, 2/b. ábra elrendezésében teljesül, a negyedik fivér örökségének a területe csak 3 egységnyi, azaz 540 m

^{2}

lehet.

3. ábra

Meg kell még mutatnunk, hogy ez az eredmény lehetséges, nincsen olyan további feltétel, ami kizárná. Ehhez megadunk egy konvex négyszöget, amelyben az egyes résznégyszögek területe rendre 2, 4, 5 és 3 egység.
Induljunk ki egy olyan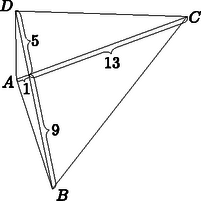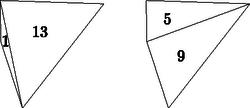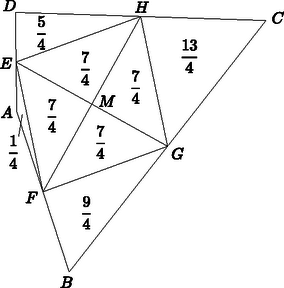

A B C D

négyszögből, amelynek az átlói

5 : 9

, illetve

1 : 13

arányban osztják egymást a 4. ábra szerint. Ilyen konvex négyszög nyilván szerkeszthető. Ekkor

\frac{[A B D]}{[C D B]} = \frac{1}{13}

, ugyanis a két háromszög közös

B D

alapjához tartozó magasságok aránya ugyancsak

1 : 13

. Hasonlóan kapjuk, hogy

\frac{[A C D]}{[C A B]} = \frac{5}{9}

. Ha tehát az

A B C D

négyszög területe 14 egység, akkor az átlói az 5. ábrán látható módon osztják 1 és 13, illetve 5 és 9 egységnyi területű háromszögekre. A négyszög oldalfelező pontjait összekötő szakaszok ezekben a háromszögekben középvonalak, ezért az

A B C D

négyszög csúcsainál keletkező háromszögek területe ezeknek az értékeknek a negyede. Végül a

\frac{t}{2} = 7

egységnyi területű

E F G H

paralelogrammát az átlói

\frac{7}{4}

területű háromszögekre osztják (6. ábra). Az egyes részek területe így valóban

\begin{matrix} = [E A F] + [E F M] = \frac{1}{4} + \frac{7}{4} = 2, \\ [M F B G] & = [F B G] + [F G M] = \frac{9}{4} + \frac{7}{4} = 4, \\ [M G C H] & = [G C H] + [G H M] = \frac{13}{4} + \frac{7}{4} = 5, végül \\ [M H D E] & = [H D E] + [H E M] = \frac{5}{4} + \frac{7}{4} = 3. \end{matrix}

A negyedik testvérnek tehát 540 m

^{2}

rész jutott.

4. ábra

5. ábra

6. ábra