Kezdőlap


Feladat:	3634. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szász Krisztián
Füzet:	2004/március, 184 - 185. oldal		PDF \| MathML
Témakör(ök):	Izotermikus állapotváltozás (Boyle--Mariotte-törvény), Hidrosztatikai nyomás, Feladat
Hivatkozás(ok):	Feladatok: 2003/szeptember: 3634. fizika feladat

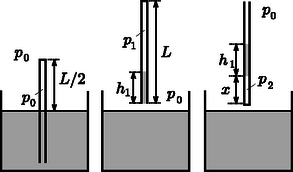
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Kezdetben az $L$ hosszú csőben levő levegő nyomása a külső légnyomással $(p_{0})$ egyezik meg, hiszen a cső nyitott. Ugyanennyi a nyomás akkor is, amikor a félig vízbe merülő cső felső végét befogjuk (bal oldali ábra).
Kiemelés után a csőben $h_{1}$ magasságú vízoszlop marad, és a bezárt levegő nyomása $p_{1}$ (középső ábra). A hőmérséklet a folyamat során állandónak tekinthető; vagy ha változik is, gyorsan visszaáll a környezet hőmérsékletére. A Boyle‐Mariotte-törvény szerint

\begin{matrix} p_{0} \frac{L}{2} = p_{1} (L - h_{1}), \end{matrix}

(1)

továbbá a vízoszlop mechanikai egyensúlyának feltételéből

\begin{matrix} p_{1} = p_{0} - ϱ g h_{1} . \end{matrix}

(2)

A cső megfordítása után a jobb oldali ábrán látható helyzet alakul ki. Ismét felírhatjuk a Boyle‐Mariotte-törvényt a cső végébe zárt levegőre:

\begin{matrix} p_{0} \frac{L}{2} = p_{2} x, \end{matrix}

(3)

illetve az erőegyensúly feltételét a vízoszlopra:

\begin{matrix} p_{2} = p_{0} + ϱ g h_{1} . \end{matrix}

(4)

Az (1) és (2) egyenletekből

p_{1}

kiküszöbölése után a

\begin{matrix} h_{1}^{2} - h_{1} (L + \frac{p_{0}}{ϱ g}) + \frac{p_{0} L}{2 ϱ g} = 0 \end{matrix}

másodfokú egyenletet kapjuk, melynek fizikailag értelmes megoldása:

h_{1} = 47, 6 cm

. Ezt behelyettesítve a (3) és (4) egyenletekből kapható

\begin{matrix} x = \frac{p_{0} L}{2 (p_{0} + ϱ g h_{1})} \end{matrix}

összefüggésbe a beszorult levegő hosszára végül

x = 47, 8 cm

adódik.