Kezdőlap


Feladat:	B.3596	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Koltai Péter
Füzet:	2003/október, 416 - 417. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Körülírt kör, Körérintők, Háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2002/december: B.3596

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $k_{i}$ kör középpontját $O_{i}$ -vel jelölve az $O_{1} O_{2} O_{3}$ háromszög oldalaira $O_{1} O_{2} = 3 R$ , $O_{1} O_{3} = 4 R$ , $O_{2} O_{3} = 5 R$ adódik, mert érintkező körök esetén az érintési pont és a körök középpontjai egy egyenesre illeszkednek. A háromszög $O_{1}$ -nél lévő szöge tehát Pitagorasz tételének megfordításából következően derékszög. Ezért a háromszög területe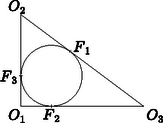

\begin{matrix} T = \frac{O_{1} O_{2} \cdot O_{1} O_{3}}{2} = 6 R^{2} . \end{matrix}

Mivel a háromszög kerülete

\begin{matrix} 2 s = O_{1} O_{2} + O_{2} O_{3} + O_{3} O_{1} = 12 R, \end{matrix}

a háromszögbe írható kör sugara

r = \frac{T}{s} = R

2. ábra

Jelölje az

O_{1} O_{2} O_{3}

háromszög beírt körének az oldalakon lévő érintési pontjait a 2. ábrán látható módon

F_{1}

F_{2}

és

F_{3}

. Ismert (lásd pl. Kiss Gy.: Amit jó tudni a háromszögekről, KöMaL 2002/3, 130‐139. old), hogy ekkor

\begin{matrix} \begin{matrix} O_{1} F_{2} & = O_{1} F_{3} = s - O_{2} O_{3} = 6 R - 5 R = R, \\ O_{2} F_{1} & = O_{2} F_{3} = s - O_{1} O_{3} = 6 R - 4 R = 2 R, \\ O_{3} F_{2} & = O_{3} F_{1} = s - O_{1} O_{2} = 6 R - 3 R = 3 R . \end{matrix} \end{matrix}

Ez viszont azt jelenti, hogy az

F_{i}

(

i = 1,2,3

) pontok egybeesnek az

E_{i}

pontokkal. Vagyis az

O_{1} O_{2} O_{3}

háromszög beírt köre átmegy az

E_{i}

pontokon, azaz megegyezik az

E_{1} E_{2} E_{3}

háromszög köré írt körrel.
Ezért az

E_{1} E_{2} E_{3}

háromszög köré írt körének sugara

R

, tehát ez a kör egybevágó

k_{1}

-gyel.

() Koltai Péter (Révkomárom, Selye J. Gimn., 12. évf.) dolgozata alapján

II. megoldás. Miután beláttuk, hogy az

O_{2} O_{1} O_{3}

szög derékszög, a következő úton is befejezhetjük a bizonyítást:
Mivel

O_{1} E_{3} = O_{1} E_{2} = R

, azért az

O_{1} E_{2} E_{3}

derékszögű háromszögben

E_{2} E_{3} = \sqrt[]{2} R

. Az

E_{2} O_{3} E_{1}

és

E_{3} O_{2} E_{1}

egyenlő szárú háromszögek szárszögeinek összege

90^{\circ}

, tehát az alapon fekvő szögeik összege ‐ az 1. ábra jelöléseit használva ‐

2 α + 2 β = 270^{\circ}

és így

\begin{matrix} E_{3} E_{1} E_{2} ∢ = 180^{\circ} - (α + β) = 180^{\circ} - \frac{270^{\circ}}{2} = 45^{\circ} . \end{matrix}

E_{1} E_{2} E_{3}

háromszög köré írt kör sugarát

R_{E}

-vel jelölve az ismert képlet alapján kapjuk, hogy

\sqrt[]{2} R = E_{2} E_{3} = 2 R_{E} sin 45^{\circ}

, ahonnan

R_{E} = R

adódik, ami éppen a bizonyítandó állítás.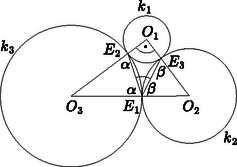