Kezdőlap


Feladat:	B.3588	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Backhausz Ágnes , Baráth Géza , Bérczi Kristóf , Birkus Róbert , Eckert Bernadett , Fehér Gábor , Gehér György , Hartmann Zoltán , Hubai Tamás , Jelitai Kálmán , Király Csaba , Kiss-Tóth Christián , Komjáthy Júlia , Koreck Péter , Mészáros Tamás , Molnár András , Pongrácz András , Rácz Judit , Salát Máté , Sándor Ágnes , Sándor Nóra Katalin , Sparing Dániel , Szabó Botond , Szijártó András , Tábor Áron , Torma Róbert
Füzet:	2003/április, 223 - 226. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Kör geometriája, Pitagorasz-tétel alkalmazásai, Thalesz tétel és megfordítása, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 2002/november: B.3588

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje $H$ a keresett ponthalmazt, $O$ a kör középpontját, $r$ pedig a sugarát. Ha $F \in H$ , akkor $O F$ merőleges az $A B$ húrra, így Pitagorasz tétele szerint $O F^{2} + A F^{2} = O A^{2} = r^{2}$ (1. ábra). A derékszögű $A M B$ háromszögben $F$ az átfogó felezőpontja, ezért $A F = F M$ , és így

\begin{matrix} O F^{2} + F M^{2} = r^{2} . \end{matrix}

(1)

Állítjuk, hogy a talált feltétel elégséges: ha a sík egy adott

F

pontjára teljesül (1), akkor

F \in H

. Először is megmutatjuk, hogy ekkor

F

a kör középpontjától különböző belső pont, azaz

0 < O F < r

. (1) miatt nyilván

0 \leq O F \leq r

. Ha itt

O F = 0

, azaz

O = F

, akkor

F M = O M = r

, ami nem lehet, hiszen az

M

belső pont. Hasonlóan, ha

O F = r

, akkor

F M = 0

F

és

M

esnek egybe és ismét

O M = r

adódik.

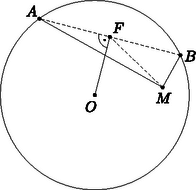1. ábra

Létezik tehát az

O F

-re

F

-ben merőleges egyenes és két pontban metszi a kört. Ha ez a szelő az

A B

húr, akkor az

F

pont felezi, így a Pitagorasz-tételből

A F^{2} = r^{2} - O F^{2}

, ami (1) szerint éppen

F M^{2}

. Így

F A = F M = F B

, és mivel

A

B

és

M

különböző pontok, a létrejövő

A M B

háromszögben az

M

csúcsnál valóban derékszög van.
Azt kell tehát tisztáznunk, hogy mi azoknak az

F

pontoknak a mértani helye, amelyekre (1) teljesül, azaz amelyek két adott ponttól mért távolságának négyzetösszege állandó. Ezt megtehetnénk koordinátageometriai eszközökkel, azonban egy hasznos eredmény, az úgynevezett paralelogramma-tétel gyors befejezést tesz lehetővé.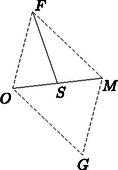

Tétel. Egy paralelogrammában az oldalak négyzetösszege az átlók négyzetösszegével egyenlő. (A tétel a Geometriai feladatok gyűjteménye II. 289. feladata.)

2. ábra

Tükrözzük az

O F M

háromszöget az

O M

szakasz

S

felezőpontjára (2. ábra). Így az

O F M G

paralelogrammát kapjuk. Ha

O M = d

, akkor a paralelogramma-tétel szerint a sík tetszőleges

F

pontjára

\begin{matrix} 2 (O F^{2} + F M^{2}) = O M^{2} + F G^{2} = d^{2} + 4 F S^{2} . \end{matrix}

Rendezés után

\begin{matrix} F S^{2} = \frac{1}{4} (2 (O F^{2} + F M^{2}) - d^{2}), \end{matrix}

(2)

tehát (1) pontosan akkor teljesül az

F

pontra, ha

F S^{2} = \frac{1}{4} (2 r^{2} - d^{2})

. Ez pedig akkor és csak akkor igaz, ha

F

S

középpontú,

\frac{\sqrt[]{2 r^{2} - d^{2}}}{2}

sugarú körön van.
Mivel minden egyes lépésben szükséges és elégséges feltételt adtunk meg, a keresett mértani hely egy kör, amelynek középpontja az

O M

szakasz felezőpontja, sugara pedig

\frac{\sqrt[]{2 r^{2} - d^{2}}}{2}

() Backhausz Ágnes (Budapest, Fazekas Mihály Gimn., 12. évf.)

Megjegyzés. Ha adottak a síkon az

A_{1}, A_{2}, ..., A_{n}

pontok és egy

P_{0}

pont, akkor akár a paralelogrammatétel ismételt alkalmazásával, akár koordinátageometriai eszközökkel egyszerűen igazolható, hogy azon

P

pontok mértani helye, amelyekre

\begin{matrix} A_{1} P^{2} + A_{2} P^{2} + ... + A_{n} P^{2} = A_{1} P_{0}^{2} + A_{2} P_{0}^{2} + ... + A_{n} P_{0}^{2} \end{matrix}

egy olyan kör, amelynek a középpontja az

A_{1}, A_{2}, ..., A_{n}

pontrendszer

S

súlypontja és a kör átmegy a

P_{0}

ponton. Ha pedig azt kérdezzük, hogy mi azon

P

pontok mértani helye, amelyekre az

A_{1} P^{2} + A_{2} P^{2} + ... + A_{n} P^{2}

négyzetösszeg állandó, akkor a válasz ennek az állandónak az értékétől függően egy

S

középpontú kör, az

S

pont, vagy pedig üres halmaz.

II. megoldás. A megoldásban felhasználjuk az alábbi segédtételt:

Ha az

A B C D

négyszög téglalap, akkor a sík ‐ valójában a tér ‐ tetszőleges

P

pontjára

P A^{2} + P 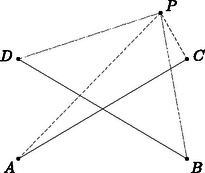C^{2} = P B^{2} + P D^{2}

(3. ábra).

3. ábra

Ez az állítás az I. megoldásban kimondott paralelogramma-tételből következik. Annak (2) alakja szerint ugyanis egy pontot egy szakasz két végpontjával összekötő szakaszok négyzetösszege kizárólag a szakasz hosszától és a pontnak a szakasz felezőpontjától mért távolságától függ. Mivel egy téglalap átlói egyenlő hosszúak, a felezőpontjuk pedig egybeesik, az állítás valóban igaz.
Tekintsük most az

M

csúcsú derékszög egy adott helyzetét, és egészítsük ki az

A M B

háromszöget téglalappá (4. ábra). Legyen ennek a téglalapnak a negyedik csúcsa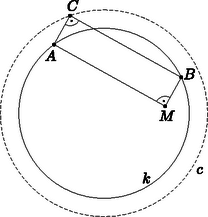

C

4. ábra

Ekkor a fenti állítást az adott ‐ és a továbbiakban

k

-val jelölt ‐ kör

O

középpontjára és erre a téglalapra alkalmazva

O M^{2} + O C^{2} = O A^{2} + O B^{2} = 2 r^{2}

. Ez azt jelenti, hogy a derékszöggel együtt forgó

C

pont állandó távolságra van a

k

kör

O

középpontjától:

\begin{matrix} O C^{2} = 2 r^{2} - d^{2} . \end{matrix}

(3)

(Az előző megoldás szerint az

O M

szakasz hossza

d

.)
Megmutatjuk, hogy az így adódó,

k

-val koncentrikus

c

kör minden

C

pontjához van az

M

körül forgó derékszögnek olyan helyzete, hogy a 4. ábra szerint kapott téglalap negyedik csúcsa éppen

C

. Próbáljuk ehhez megszerkeszteni a megfelelő téglalapot.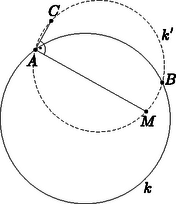

5. ábra

Mivel

d < r

, azért (3)-ból

O C > r

adódik, a

C

tehát külső pontja a

k

körnek. A feltétel szerint viszont az

M

belső pont, így pedig az

M C

átmérőjű

k'

kör két pontban metszi

k

-t. Legyenek ezek

A

és

B

. (5. ábra). Meg kell mutatnunk, hogy az így szerkesztett

C A M B

négyszög valóban téglalap.
Thalész tétele szerint

C A M ∢ = 90^{\circ}

, van tehát olyan

B'

pont, amelyre a

C A M B'

négyszög téglalap (6. ábra). Ennek a körülírt köre a

C A M

háromszög körülírt köre, azaz

k'

. A megoldás elején kimondott állítást most erre a

C A M B'

téglalapra és az

O

pontra alkalmazva (3) felhasználásával kapjuk, hogy

\begin{matrix} {O B'}^{2} = O C^{2} + O M^{2} - O A^{2} = (2 r^{2} - d^{2}) + d^{2} - r^{2} = r^{2} . \end{matrix}

6. ábra

B'

pont tehát a

k

körön is rajta van, és így nem más, mint a

k

és

k'

körök

A

-tól különböző metszéspontja, a

B

pont. Ez pedig éppen azt jelenti, hogy a

C A M B

négyszög azonos a

C A M B'

téglalappal.
A

C

pontok mértani helye tehát az

O

középpontú,

\sqrt[]{2 r^{2} - d^{2}}

sugarú

c

kör. Mivel

F

a szóban forgó téglalap

A B

átlójának a felezőpontja, azért felezi az

M C

átlót is. A keresett ponthalmaz tehát az

M C

szakaszok felezőpontjainak a mértani helye, miközben a

C

pont befutja a

c

kört: éppen a

c

körnek az

M

pontból felére kicsinyített képe. Az

F

pontok mértani helye tehát egy

\frac{\sqrt[]{2 r^{2} - d^{2}}}{2}

sugarú kör, melynek középpontja az

O M

szakasz felezőpontja.

() Pongrácz András (Szolnok, Verseghy Ferenc Gimn., 11. évf.) ötlete alapján