Feladat: B.3546 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 2002/december, 543 - 544. oldal  PDF  |  MathML 
Témakör(ök): Kocka, Térgeometriai bizonyítások, Szimmetrikus sokszögek, Feladat
Hivatkozás(ok):Feladatok: 2002/április: B.3546

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hatszög különböző oldalainak a kocka különböző lapjain kell lenniük, szemközti oldalaknak szemközti lapokon. Ha két párhuzamos síkot elmetszünk egy harmadikkal, akkor a keletkező két metszésvonal is párhuzamos. Mivel a kocka szemközti lapsíkjai párhuzamosak, azért az ABCDEF hatszög szemközti oldalai is párhuzamosak (1. ábra).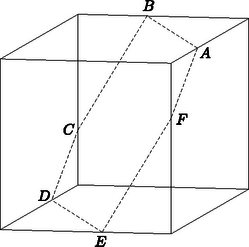

 
 

1. ábra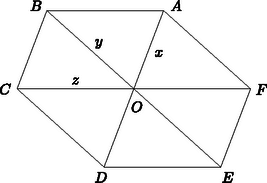
 

 

2. ábra
 

Legyen a hatszög átlóinak metszéspontja O, az oldalak hossza a 2. ábrán látható módon a, b, c, d, e és f, továbbá legyen OA=x, OB=y és OC=z. Mivel AB∥DE, a párhuzamos szelők tételéből következik, hogy
OD=d⋅xaésOE=d⋅ya.
Ugyanígy kapjuk EF és BC párhuzamosságát felhasználva, hogy
OE=e⋅ybésOF=e⋅zb,
FA és CD párhuzamosságából pedig, hogy
OF=f⋅zcésOD=c⋅xf.
Összeszorozva az első, illetve a második oszlopban lévő egyenlőségeket
d⋅xa⋅e⋅yb⋅f⋅zc=OD⋅OE⋅OF=d⋅ya⋅e⋅zb⋅c⋅xf
adódik, amiből egyszerűsítés után kapjuk, hogy
fc=cf,
tehát f=c. Hasonlóan kapjuk, hogy e=b és d=a. Ez azt jelenti, hogy a hatszög középpontosan szimmetrikus, a középpontja O.
Megmutatjuk, hogy O egyúttal a kocka középpontja is. Tükrözzük a kocka AB egyenest tartalmazó S lapsíkját O-ra. A tükörkép az az S' sík lesz, amely párhuzamos S-sel, és átmegy AB tükörképén, azaz a DE egyenesen. Ez a sík tehát éppen a kocka S-sel párhuzamos lapsíkja. Ebből következik, hogy O egyenlő távolságra van a kocka AB-t, illetve DE-t tartalmazó párhuzamos lapjaitól. Ugyanígy kapjuk, hogy O a kocka másik két pár párhuzamos lapjától is egyenlő távolságra van, tehát valóban a kocka középpontja.
A hatszög síkja tehát áthalad a kocka középpontján, és ez a pont egyúttal a hatszögnek is szimmetriacentruma.