Kezdőlap


Feladat:	B.3523	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Konfár András
Füzet:	2002/november, 483 - 485. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Szélsőérték-feladatok differenciálszámítás nélkül, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2002/február: B.3523

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje a körülírt háromszög félkört érintő oldalait $a$ és $b$ . A félkör $O$ középpontját a háromszög szemközti csúcsával összekötő szakasz a háromszöget két olyan háromszögre bontja, melyeknek az $a$ illetve $b$ oldalához tartozó magassága $r$ , a félkör sugara (1. ábra) Ennek megfelelően a háromszög kétszeres területe: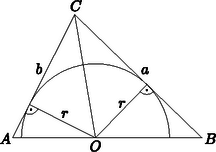

\begin{matrix} 2 T = (a + b) \cdot r . \end{matrix}

1. ábra

A számtani és mértani közép közti egyenlőtlenség szerint

a + b \geq 2 \sqrt[]{a b}

; ennek felhasználásával a fenti egyenlőségből az alábbi becslést kapjuk:

\begin{matrix} T \geq r \sqrt[]{a b} . \end{matrix}

(1)

Jegyezzük meg, hogy itt pontosan akkor van egyenlőség, ha

a = b

, a háromszög egyenlő szárú.

Megjegyzés. Láthatóan elegendő az egyenlő szárú körülírt háromszögek közül megkeresni a minimális területűt, ez az út viszont váratlan problémákat vet föl. A fentiekből egészen pontosan annyi következik, hogy az

a \neq b

oldalú körülírt háromszögnél biztosan kisebb területű az egyenlő,

\frac{a + b}{2}

-szárú körülírt háromszög ‐ ha ez utóbbi létezik. Egy szerencsés további becsléssel ez a vizsgálat elkerülhető.

A háromszög kétszeres területére fennálló

2 T = a b sin γ

összefüggésből

0 < sin γ \leq 1

miatt

a b \geq 2 T

adódik, és pontosan akkor van egyenlőség, ha az

a

és

b

oldalak szöge derékszög. Az (1) egyenlőtlenég jobb oldala tehát alulról becsülhető: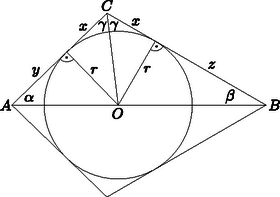

r \sqrt[]{a b} \geq r \sqrt[]{2 T}

és így a

\begin{matrix} T \geq r \sqrt[]{2 T} \end{matrix}

egyenlőtlenséget kapjuk. Négyzetre emelve és

T

-vel osztva

T \geq 2 r^{2}

és láttuk, hogy pontosan akkor van egyenlőség, ha a háromszög egyenlő szárú és derékszögű.

2. ábra

II. megoldás. Jelölje

T

a háromszög területét. Tükrözzük a háromszöget a félkör átmérőjére (2. ábra). Az így kapott deltoid érintőnégyszög, területe tehát a beírt kör sugarának és a kerület felének a szorzata. Használjuk az ábra jelöléseit: az érintő szakaszok hossza

\begin{matrix} \begin{matrix} x = r \cdot ctg γ; y = r \cdot ctg α; \\ z = r \cdot ctg β . \end{matrix} \end{matrix}

Innen

\begin{matrix} 2 T = r \frac{4 x + 2 y + 2 z}{2} = r^{2} (2 ctg γ + ctg α + ctg β) . \end{matrix}

α

β

és

γ

egy konvex négyszög egy-egy szögének a fele, így mindegyikük hegyesszög. A kotangens függvény konvex a

] 0; \frac{π}{2}]

intervallumon, így a Jensen egyenlőtlenség szerint:

\begin{matrix} \frac{2 ctg γ + ctg α + ctg β}{4} \geq ctg \frac{2 γ + α + β}{4} = ctg \frac{π}{4} = 1. \end{matrix}

Így

2 T = r^{2} (2 ctg γ + ctg α + ctg β) \geq 4 r^{2}

, egyenlőség pedig pontosan akkor teljesül, ha

α = β = γ = 45^{\circ}

, a minimális területű körülírt háromszög tehát egyenlő szárú és derékszögű.

Konfár András (Szeged, Radnóti Miklós Gimn., 10. évf.)