Kezdőlap


Feladat:	B.3519	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Barabás László
Füzet:	2002/október, 418. oldal		PDF \| MathML
Témakör(ök):	Tetraéderek, Térelemek és részeik, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 2002/január: B.3519

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $P$ az $A_{1} A_{3}$ , $B_{1} B_{3}$ és $C_{1} C_{3}$ egyenesek, $Q$ pedig az $A_{1} A_{2}$ , $B_{1} B_{2}$ és $C_{1} C_{2}$ egyenesek közös pontja (lásd az ábrát). Vizsgáljuk meg a $P Q$ egyenes és az $S = O A_{2} A_{3}$ sík kölcsönös helyzetét. $P Q$ nincs benne $S$ -ben, mert ellenkező esetben az $A_{1} = P A_{3} \cap Q A_{2}$ pont is $S$ -beli volna, azaz $O A_{1} A_{2} A_{3}$ nem lenne tetraéder.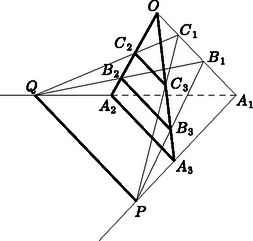

Tegyük fel, hogy

P Q

M

pontban döfi

S

-et. Ekkor

M

benne van az

S_{A} = A_{1} P Q

, az

S_{B} = B_{1} P Q

és az

S_{C} = C_{1} P Q

síkokban is. Ezért

M

rajta van az

S

és az

S_{A}

síkok metszésvonalán, vagyis az

A_{2} A_{3}

egyenesen. Ugyanígy

M

rajta van az

S \cap S_{B} = B_{2} B_{3}

és az

S \cap S_{C} = C_{2} C_{3}

egyeneseken is. Ekkor pedig az

A_{2} A_{3}

B_{2} B_{3}

és

C_{2} C_{3}

egyenesek valóban egy ponton ‐

M

-en ‐ mennek át.
Tegyük most fel, hogy

P Q

párhuzamos az

S

síkkal. Ekkor

P Q

-nak és az

S

-beli

A_{2} A_{3}

egyenesnek nem lehet közös pontja. De

P Q

és

A_{2} A_{3}

benne vannak az

S_{A}

síkban, ezért ha nincs közös pontjuk, akkor párhuzamosak. Ugyanígy láthatjuk be ‐ az

S_{B}

, illetve az

S_{C}

síkok segítségével ‐, hogy

B_{2} B_{3}

és

C_{2} C_{3}

is párhuzamos

P Q

-val. Ez viszont azt jelenti, hogy az

A_{2} A_{3}

B_{2} B_{3}

és

C_{2} C_{3}

egyenesek egymással is párhuzamosak.
Mivel más eset nincs, a feladat állítását beláttuk.

Barabás László (Bonyhád, Petőfi S. Ev. Gimn., 9. évf.) dolgozata alapján

Megjegyzés. Ismert, hogy ha három sík páronként egy-egy egyenesben metszi egymást, akkor a három metszésvonal vagy egy ponton megy át, vagy párhuzamos (lásd pl. Geometriai feladatok gyűjteménye I. kötet, 1703‐04. feladatok). Megoldásunk gondolatmenete lényegében megegyezik ennek az állításnak a bizonyításával.