Feladat:	B.3484	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baráth Géza ,  Bóka Gergely ,  Borgátai Diána ,  Dénes Ferenc ,  Erdős Dóra ,  Filus Tamás ,  Kajtár Máté ,  Klobb Maja ,  Kovács Dóra Judit ,  Maga Péter ,  Márton Sándor ,  Mosolygó György ,  Nyul Balázs ,  Oláh Zsolt ,  Pongrácz András ,  Salát Máté ,  Slíz György ,  Strenner Balázs ,  Szabó Áron ,  Szemjon Viktória ,  Szücs András ,  Tulokdi Áron
Füzet:	2002/április, 219 - 220. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 2001/október: B.3484

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $\text{ctg}\frac{\alpha }{2}=n$, $\text{ctg}\frac{\beta }{2}=n-1$, $\text{ctg}\frac{\gamma }{2}=n-2$, ahol $n$ egész szám. Megmutatjuk, hogy a feladat feltételeit (hasonlóság erejéig) legfeljebb egy háromszög elégítheti ki. Tegyük fel ugyanis, hogy az $\alpha \text{'}$, $\beta \text{'}$, $\gamma \text{'}$ szögű háromszög is megfelelő, azaz alkalmas $k$ egésszel $\text{ctg}\frac{\alpha \text{'}}{2}=k$, $\text{ctg}\frac{\beta \text{'}}{2}=k-1$, $\text{ctg}\frac{\gamma \text{'}}{2}=k-2$. A háromszögek félszögei a $\left(\mathrm{0,}\frac{\pi }{2}\right)$ intervallumhoz tartoznak, ott pedig a $\text{ctg}x$ függvény szigorúan monoton fogyó. Ha föltesszük, hogy $k=n$, akkor $\text{ctg}\frac{\alpha \text{'}}{2}=\text{ctg}\frac{\alpha }{2}$ miatt $\alpha \text{'}=\alpha$, és ugyanígy $\beta \text{'}=\beta$ és $\gamma \text{'}=\gamma$. Ha nem ez a helyzet, akkor föltehető, hogy $k>n$. Ekkor viszont $\text{ctg}\frac{\alpha \text{'}}{2}>\text{ctg}\frac{\alpha }{2}$ miatt $\alpha \text{'}<\alpha$, és $\beta \text{'}<\beta$ és $\gamma \text{'}<\gamma$, ami lehetetlen.     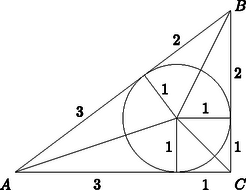Elegendő tehát egyetlen olyan háromszöget találni, ami teljesíti a feltételeket. Az ábráról könnyen leolvasható, hogy ilyen az a derékszögű háromszög, amelynek oldalai 3, 4, 5. Ennek legnagyobb szöge $\gamma =\frac{\pi }{2}$. Filus Tamás (Szeged, Radnóti M. Kísérleti Gimn., 9. évf.) megoldása   II. megoldás. Az előző megoldás jelöléseit használjuk. A tangensfüggvényre vonatkozó addíciós képlet szerint $\begin{array}{c}{\displaystyle \text{ctg}\frac{\beta }{2}=\text{ctg}\left(\frac{\pi }{2}-\frac{\alpha +\gamma }{2}\right)=\text{tg}\left(\frac{\alpha }{2}+\frac{\gamma }{2}\right)=\frac{\text{tg}\frac{\alpha }{2}+\text{tg}\frac{\gamma }{2}}{1-\text{tg}\frac{\alpha }{2}\text{tg}\frac{\gamma }{2}}\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle n-1=\frac{\frac{1}{n}+\frac{1}{n-2}}{1-\frac{1}{n\left(n-2\right)}}}& {\displaystyle =\frac{2\left(n-1\right)}{n^2-2n-1}\mathrm{,}}\hfill \\ \hfill {\displaystyle }\\ \hfill {\displaystyle n^2-2n-1}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle }\\ \hfill {\displaystyle \left(n-3\right)\left(n+1\right)}& {\displaystyle =0.}\hfill \end{array}}}\end{array}$ Mivel egy háromszög bármelyik szögének a fele $0$ és $\frac{\pi }{2}$ közé esik és az ilyen szögek kotangense pozitív, az egyetlen megoldás $n=3$, tehát a legnagyobb szögre $\text{ctg}\frac{\gamma }{2}=1$, vagyis $\gamma$ derékszög. Szemjon Viktória (Kárpátalja, Jánosi, Jánosi Középiskola, 11. évf.)