Kezdőlap


Feladat:	B.3478	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Rátz Judit , Sásdy Gabriella
Füzet:	2002/március, 159 - 161. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Háromszög területe, Hozzáírt körök, Síkgeometriai számítások trigonometriával, Jensen-féle egyenlőtlenség, Feladat
Hivatkozás(ok):	Feladatok: 2001/szeptember: B.3478

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat megoldásai során az e szám 130‐138. oldalain megtalálható ,,Amit jó tudni a háromszögekről" című cikkben szereplő jelöléseket és eredményeket használjuk.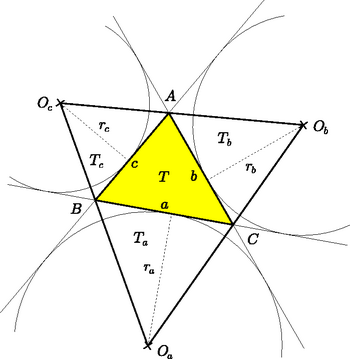

1. ábra

I. megoldás. Az

O_{a} O_{b} O_{c}

háromszög területe megegyezik az

A B C

O_{a} B C

O_{b} C A

és

O_{c} A B

háromszögek területének összegével (1. ábra). Ezért azt kell megmutatnunk, hogy

\begin{matrix} T + \frac{a \cdot r_{a}}{2} + \frac{b \cdot r_{b}}{2} + \frac{c \cdot r_{c}}{2} \geq 4 T . \end{matrix}

Ezt rendezve és a 8. állítást felhasználva a bizonyítandó egyenlőtlenség:

\begin{matrix} a \cdot \frac{T}{s - a} + b \cdot \frac{T}{s - b} + c \cdot \frac{T}{s - c} \geq 6 T, azaz \frac{a}{s - a} + \frac{b}{s - b} + \frac{c}{s - c} \geq 6. \end{matrix}

Mivel

\frac{a}{s - a} = \frac{s}{s - a} - 1

\frac{b}{s - b} = \frac{s}{s - b} - 1

és

\frac{c}{s - c} = \frac{s}{s - c} - 1

, elég azt megmutatni, hogy

\begin{matrix} \frac{s}{s - a} + \frac{s}{s - b} + \frac{s}{s - c} \geq 9, \end{matrix}

illetve hogy az ennek átrendezésével kapott

\begin{matrix} \frac{\frac{1}{s - a} + \frac{1}{s - b} + \frac{1}{s - c}}{3} \geq \frac{3}{s} \end{matrix}

egyenlőtlenség fennáll. Ez utóbbi viszont következik a számtani és a harmonikus közepek közti egyenlőtlenségből, mert aszerint:

\begin{matrix} \frac{3}{\frac{1}{s - a} + \frac{1}{s - b} + \frac{1}{s - c}} \leq \frac{(s - a) + (s - b) + (s - c)}{3} = \frac{s}{3} . \end{matrix}

Sásdy Gabriella (Szentendre, Ferences Gimn., 12. évf.) dolgozata alapján

II. megoldás. Írjuk fel az

O_{a} O_{b} O_{c}

háromszög területét ugyanúgy, mint az I. megoldásban:

\begin{matrix} T_{O_{a} O_{b} O_{c}} = s \cdot r + \frac{a \cdot r_{a}}{2} + \frac{b \cdot r_{b}}{2} + \frac{c \cdot r_{c}}{2} . \end{matrix}

A 8. állításból következik, hogy

s \cdot r = (s - a) r_{a}

, azaz

a \cdot r_{a} = s \cdot r_{a} - s \cdot r

. Ezért

2 T_{O_{a} O_{b} O_{c}} = s r + (s r_{a} - s r) + (s r_{b} - s r) + (s r_{c} - s r) = s (r_{a} + r_{b} + r_{c} - r) .

Vagyis a 10. állítást felhasználva:

2 T_{O_{a} O_{b} O_{c}} = s \cdot 4 R

, azaz

T_{O_{a} O_{b} O_{c}} = 2 R s .

A 12. állítás szerint

R \geq 2 r

, tehát

T_{O_{a} O_{b} O_{c}} = 2 \cdot R \cdot s \geq 2 \cdot 2 \cdot r \cdot s = 4 T

, ami éppen a bizonyítandó állítás.

Rácz Judit (Szekszárd, Garay J. Gimn., 11. évf.) dolgozata alapján

III. megoldás. Az 5. állítás szerint az

O_{a} O_{b} O_{c}

háromszög szögei

\frac{α + β}{2}

\frac{β + γ}{2}

és

\frac{γ + α}{2}

, a 7. következmény szerint pedig az e háromszög köré írható kör sugara

2 R

. Ezért a 3. állítás alapján

\begin{matrix} T_{O_{a} O_{b} O_{c}} = 2 \cdot {(2 R)}^{2} \cdot sin \frac{α + β}{2} \cdot sin \frac{β + γ}{2} \cdot sin \frac{γ + α}{2} . \end{matrix}

Mivel

α + β + γ = 180^{\circ}

, ezért

\frac{α + β}{2} = 90^{\circ} - \frac{γ}{2}

\frac{β + γ}{2} = 90^{\circ} - \frac{α}{2}

és

\frac{γ + α}{2} = 90^{\circ} - \frac{β}{2}

, tehát

sin \frac{α + β}{2} \cdot sin \frac{β + γ}{2} \cdot sin \frac{γ + α}{2} = cos \frac{α}{2} \cdot cos \frac{β}{2} \cdot cos \frac{γ}{2} .

Vagyis a 17. állítás utolsó része szerint

T_{O_{a} O_{b} O_{c}} = 8 R^{2} \cdot \frac{s \cdot T}{a b c} .

Elegendő tehát megmutatnunk, hogy

\frac{8 R^{2} \cdot s}{a b c} \geq 4

, vagyis a 2. állítást használva azt, hogy

\frac{a b c \cdot s}{2 T^{2}} \geq 4

. Ez viszont éppen a 18. állítás bizonyítása során már belátott

\frac{T^{2}}{s \cdot a b c} \leq \frac{1}{8}

egyenlőtlenség egy átrendezett alakja.