| Feladat: | B.3460 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 2002/március, 158 - 159. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek geometriája, Beírt kör, Heron-képlet, Síkgeometriai számítások trigonometria nélkül, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2001/április: B.3460 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a háromszög csúcsait és oldalait a szokásos módon , , és , , -vel; a beírt körének középpontja legyen , sugara ; a beírt körnek az oldalakon lévő érintési pontjai pedig , , (lásd az ábrát). Legyen a háromszög területe , a szakasz hossza pedig . Mivel egy külső pontból egy körhöz húzott két érintőszakasz hossza egyenlő, azért és . Vagyis , és , amiből az jelölést bevezetve kapjuk, hogy , és . 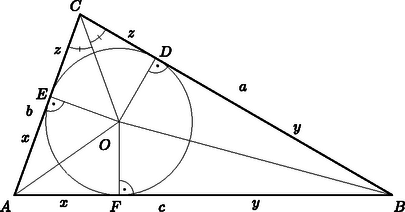 Az háromszögben -nél derékszög van, -nél lévő szöge pedig , mert az pont az háromszög belső szögfelezőinek metszéspontja. Ezért . Vagyis a bizonyítandó állítás: |