|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a félkör középpontját -val, sugarát -rel, az érintési pontot pedig -vel. Két esetet különböztetünk meg.
I. eset: (1. ábra). Mivel azért , azaz .
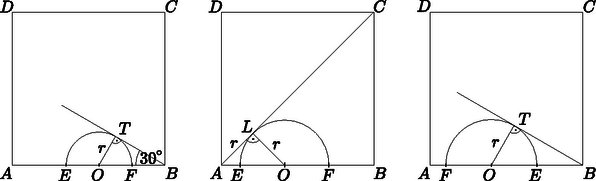 1. ábra 2. ábra 3. ábra 1. ábra 2. ábra 3. ábra
Tudjuk továbbá, hogy | |
Ekkor tehát | |
Ezt átalakítva adódik. Mivel és egészek, a 3 pedig csak négyféleképpen írható fel két egész szám szorzataként, azért csak az alábbi táblázatban szereplő értékek jöhetnek szóba:
Ezek közül csak az m=6, n=2 és az m=n=4 párok esetén lesz m is és n is pozitív, ezek adják a feladat megoldását.
Ha az AC átló is érinti a félkört, mégpedig az L pontban, akkor az AOL háromszög egyenlő szárú és derékszögű (2. ábra), ezért AO=r⋅2. De AO=AE+EO és AE=1n, EO=12(1-1n-1m)=r racionális számok, r⋅2 pedig irracionális. Ezért AC egyik esetben sem érinti a félkört.
II. eset: AE>AF (3. ábra). Az előző esethez hasonló módon kapjuk, hogy BE=r, | r=EF2=12(AE+BF-AB)=12(1n+1m-1) |
és BE=AB-AE=1-1n. Tehát 1-1n=12(1n+1m-1), azaz 3mn-3m-n=0. Ezt átalakítva (3m-1)(n-1)=1 adódik, azaz 3m-1=±1, amiből következik, hogy ebben az esetben nincs pozitív egészekből álló megoldás.
Tehát m és n kétféle értéket vehet fel: vagy m=6 és n=2, vagy pedig m=n=4. Az AC átló egyik esetben sem érinti a félkört. Dömötör Csilla (Győr, Révai M. Gimn., 11. évf.) |
 PDF |
PDF |  MathML
MathML 