Feladat:	B.3471	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gergely ,  Babos Attila ,  Balka Richárd ,  Balogh 541 János ,  Bérczi Kristóf ,  Birkner Tamás ,  Csáky Attila ,  Dányádi Zsolt ,  Hablicsek Márton ,  Hargitai Gábor ,  Kiss-Tóth Christián ,  Kocsis Albert Tihamér ,  Lovrics Anna ,  Pallos Péter ,  Paulin Dániel ,  Paulin Roland ,  Rácz Béla András ,  Simon Balázs ,  Szilágyi Zoltán ,  Tábor Áron ,  Tóth Ágnes ,  Tóth János
Füzet:	2001/október, 417 - 420. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai bizonyítások, Ellipszis egyenlete, Szöveges feladatok, Esetvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 2001/május: B.3471

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha a hangya a görbe $P\left(a;b\right)$ pontjában tartózkodik, akkor az $\begin{array}{c}{\displaystyle x^2+bx+b^2-6=0\text{és az}{y}^2+ay+a^2-6=0}\end{array}$ egyenleteknek van valós gyöke ‐ éppen $a$, illetve $b$ ‐, és így az egyenletek diszkriminánsa, $D_b=24-3b^2$ és $D_a=24-3a^2$ nem negatív. Ha valamelyikük, például $D_a=0$, azaz $|a|=2\sqrt[]{2}$ (ekkor $b=-\frac{a}{2}$), akkor a hangya az $y$ tengellyel párhuzamosan nem tud tovább haladni. Ez a két pont $Y_1\left(2\sqrt[]{2};-\sqrt[]{2}\right)$, illetve $Y_2\left(-2\sqrt[]{2};\sqrt[]{2}\right)$. Hasonlóan, amikor $D_b=0$, azaz a hangya az $X_1\left(\sqrt[]{2};-2\sqrt[]{2}\right)$ vagy az $X_2\left(-\sqrt[]{2};2\sqrt[]{2}\right)$ pontban van, akkor az $x$ tengellyel párhuzamosan nem mehet tovább. Mindez jól látható, ha meggondoljuk, hogy a szóban forgó görbe ellipszis (1. ábra), az $X_i$, $Y_i$ pontok pedig a tengelyekkel párhuzamos érintők érintési pontjai. Ha a hangya a fenti négytől különböző $P\left(a;b\right)$ görbepontban tartózkodik, akkor mindkét megengedett irányban el tud indulni. Ha $P$ nem az útvonal kezdőpontja, akkor persze csak az egyik irány mentén mehet tovább, hiszen a másik irányból kellett megérkeznie. Ha például az $x$ tengellyel párhuzamosan a görbe $Q\left(c;b\right)$ pontjába jut, akkor a fentiek szerint $c\ne a$, és ez a két szám, $a$ és $c$ az $x^2+bx+b^2-6=0$ egyenlet két valós gyöke, azaz $a+c=-b$. Hasonlóan kapjuk, hogy ha a hangya az $y$ tengellyel párhuzamos útvonalon az $R\left(a;d\right)$ pontba lép a $P$-ből, akkor $d+b=-a$ (2. ábra). Látható, hogy a hangya bármely lépésének végpontjai olyan pontok a görbén, amelyek összesen 4 koordinátájából kettő megegyezik, és ennek, valamint a további két koordinátának az összege 0, $a+b+c=0$ és $a+b+d=0$. Ha tehát a hangya például az $x$ tengellyel párhuzamosan indul el a $P_0\left(a;b\right)$ pontból, akkor útja során a következő görbepontokon halad át: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle P_0\left(a;b\right)\to P_1\left(-a-b;b\right)\to P_2\left(-a-b;a\right)\to P_3\left(b;a\right)\to }\\ \hfill {\displaystyle \to P_4\left(b;-a-b\right)\to P_5\left(a;-a-b\right)\to P_6\left(a;b\right)\mathrm{,}}\end{array}}}\end{array}$ látható tehát, hogy ha útja során nem érinti az $X_i$, $Y_i$ pontok egyikét sem, akkor pontosan a hatodik lépésben megáll. Ha útközben ezek valamelyikébe jut, akkor persze már korábban is megállhat.  Babos Attila (ELTE Radnóti M. Gyak. Gimn., 12. o.t.)   Megjegyzések. 1. Könnyen látható, hogy az $X_i$ pontokba csak az $y$ tengellyel párhuzamosan érkezhet a hangya, az $X_1$-be a $B_1\left(\sqrt[]{2};\sqrt[]{2}\right)$, az $X_2$-be pedig a $B_2\left(-\sqrt[]{2};-\sqrt[]{2}\right)$ pontból. Ugyanez a két pont ‐ azok a pontok az ellipszisen, amelyek koordinátái egyenlők ‐, ahonnan az $Y_1$ és az $Y_2$ pontokban eljuthatunk. Összefoglalva tehát, ha a hangya az $X_i$, $Y_i$, $B_i$ pontoktól különböző helyzetből indul, akkor pontosan a hatodik lépés után áll meg, a $B_i$ pontokból indulva egy, az $X_i$, $Y_i$ pontokból indulva pedig két lépés után akad el. A lényegében helyes megoldások szerzői többé-kevésbé így okoskodtak, de szinte mindenki megfeledkezett a hangya kivételes útvonalainak vizsgálatáról. 2. A $c=-a-b$ jelöléssel a hangya útvonala ‐ a kivételes pontoktól eltekintve ‐ az $\left(a;b\right)$, $\left(c;b\right)$, $\left(c;a\right)$, $\left(b;a\right)$, $\left(b;c\right)$, $\left(a;c\right)$, $\left(a;b\right)$ pontokon át vezet, a pontok koordinátái között csak az $a$, $b$, $c$ számok fordulnak elő, úgy, hogy $a+b+c=0$ (3. ábra). Maga az útvonal ‐ ahogyan a görbe is ‐ tengelyesen szimmetrikus az $y=x$ egyenletű egyenesre. Az ilyen számhármasok érdekes kapcsolatban állnak a B. 3470. feladat egy lehetséges megközelítésével. (Lásd a megjegyzést a B. 3470. feladat III. megoldásához e szám 413. oldalán.) Ha az $f\left(x\right)=x^3-6x$ harmadfokú polinomból indulunk ki (4. ábra), akkor a feladatban szereplő ellipszis egyenlete: $\begin{array}{c}{\displaystyle \frac{f\left(x\right)-f\left(y\right)}{x-y}=\mathrm{0,}}\end{array}$ az ellipszis pontjainak koordinátái pedig olyan $\left(a;b\right)$ számpárok, amelyekre $f\left(a\right)=f\left(b\right)$. A szélsőértékektől eltekintve $f$ minden többszörösen fölvett értékét háromszor veszi föl, a hangya egy adott útvonala pedig éppen egy ilyen számhármast határoz meg az út során érintett görbepontok koordinátáiként. Ebben az értelmezésben a feladat állítása nyilvánvaló.   II. megoldás. Forgassuk el a görbét ‐ és a hangya útvonalát is ‐ $\left(-{45}^{\circ }\right)$-kal, ekkor egyenlete $\frac{x^2}{12}+\frac{y^2}{4}=1$ alakú lesz (5. ábra). Az elforgatott útvonal egy, a koordinátatengelyekkel ${45}^{\circ }$-os szöget bezáró töröttvonal. Az ellipszis excentricitása, $\frac{b}{a}=\frac{1}{\sqrt[]{3}}$, így ha a görbére és a hangya útvonalára is $\sqrt[]{3}$ arányú merőleges affinitást alkalmazunk, akkor az ellipszis origó közepű körbe, a hangya útvonala pedig olyan töröttvonalba megy át, amelynek szomszédos szakaszai $60$, illetve $-{60}^{\circ }$-os szöget zárnak be az $x$ tengellyel (6. ábra). A hangya két egymást követő lépése utáni helyzetét tehát megkaphatjuk, ha útvonalának $P$ kezdőpontját ${120}^{\circ }$-kal elforgatjuk a kör kezdőpontja körül. A forgatás iránya a hangya haladási irányától függ, és mivel az utazás során ez nem változik, hat egymást követő lépés után a hangya visszajut oda, ahonnan elindult, és így valóban megáll. Mindez majdnem minden kezdőpontra teljesül annak a hat pontnak a kivételével, amelyek közül négyben az $x$ tengellyel $60$, illetve $-{60}^{\circ }$-os szöget bezáró érintők érintik a kört ‐ ezekbe a pontokba érve a hangya elakad ‐, kettő pedig a függőleges átmérő két végpontja ‐ innen juthat a hangya az érintési pontokba (7. ábra). 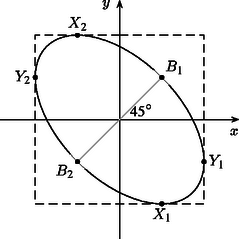 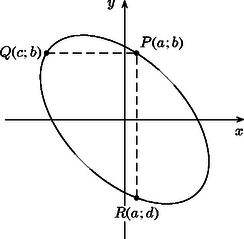 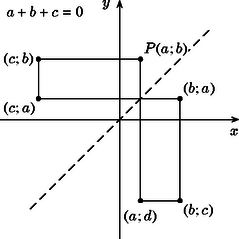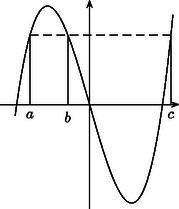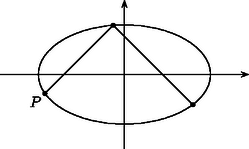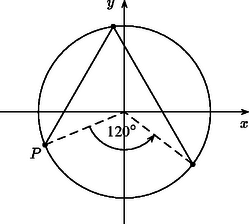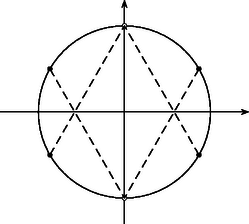Megjegyzés. A második bizonyításból nyomban adódik ‐ de a görbe egyenletét vizsgálva is kiderül ‐, hogy az állítás kizárólag az ellipszis alakján múlik, azon, hogy a kis- és a nagytengely aránya, a görbe excentricitása $1:\sqrt[]{3}$.