Feladat:	C.579	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bauer Eszter ,  Bérces Péter ,  Bérczi Kristóf ,  Bertus-Barcza Tímea ,  Besenyei Ádám ,  Birkner Tamás ,  Blastik Márta ,  Csató György ,  Csornai Gyula ,  Döme Botond ,  Erdei Zsuzsa ,  Fehér Ádám ,  Gajdos Béla ,  Hablicsek Márton ,  Klausz Ferenc ,  Kolláth Endre ,  László L. András ,  Németh Márk ,  Nyul Balázs ,  Pach Péter Pál ,  Patay Gergely ,  Sarusi Annamária ,  Tóth Ágnes ,  Varga Áron
Füzet:	2000/november, 477 - 480. oldal		PDF  |  MathML
Témakör(ök):	Egyenes körkúpok, Térfogat, Függvényvizsgálat, Kör geometriája, C gyakorlat
Hivatkozás(ok):	Feladatok: 2000/március: C.579

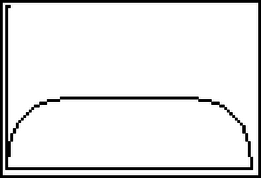
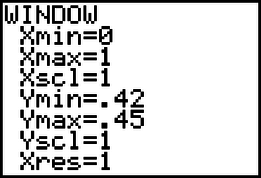
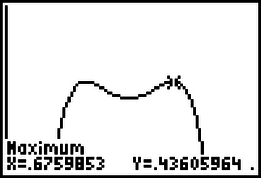
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen a körlap sugara $R$. Ha egy átmérő mentén vágjuk ketté a kört, akkor a kúp alapkörének kerülete egyenlő a félkör kerületével, vagyis $2r\pi =R\pi$, ahonnan $r=\frac{R}{2}$ az alapkör sugara, a kúpok magassága pedig $\begin{array}{c}{\displaystyle m=\sqrt[]{R^2-r^2}=\sqrt[]{R^2-{\left(\frac{R}{2}\right)}^2}=\frac{R}{2}\sqrt[]{3}\mathrm{.}}\end{array}$ A kúp kétszeres térfogata $\begin{array}{c}{\displaystyle V=2\frac{{\left(\frac{R}{2}\right)}^2\pi \frac{R}{2}\sqrt[]{3}}{3}=\frac{R^3\pi }{3}\cdot \frac{\sqrt[]{3}}{4}\approx \mathrm{0,4330127}\cdot \frac{R^3\pi }{3}\mathrm{.}}\end{array}$ Vágjuk fel ezután két tetszőleges sugár mentén a körlapot, és készítsük el a két tölcsért. A két kúp alapkörének sugara $r_1$ és $r_2$. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle i_1=\frac{R\pi \alpha }{{180}^{\circ }}\mathrm{,}}& {\displaystyle \text{ahonnan}{r}_1=\frac{R\alpha }{{360}^{\circ }}}\hfill \\ \hfill {\displaystyle i_2=2R\pi -i_1\mathrm{,}}& {\displaystyle \text{ahonnan}{r}_2=R\left(1-\frac{\alpha }{{360}^{\circ }}\right)\mathrm{.}}\hfill \end{array}}}\end{array}$ Legyen $\frac{\alpha }{{360}^{\circ }}=x$ ($0<x<1$), és írjuk fel a térfogatok összegét $x$ függvényként. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle r_1=Rx\mathrm{,}{m}_1=\sqrt[]{R^2-{\left(Rx\right)}^2}=R\sqrt[]{1-x^2}\mathrm{,}}\\ \hfill {\displaystyle V_1=\frac{{\left(Rx\right)}^2\pi \cdot R\sqrt[]{1-x^2}}{3}=\frac{R^3\pi }{3}\left(x^2\sqrt[]{1-x^2}\right)\mathrm{,}}\\ \hfill {\displaystyle r_2=R\left(1-x\right)\mathrm{,}{m}_2=\sqrt[]{R^2-R^2{\left(1-x\right)}^2}=R\sqrt[]{1-{\left(1-x\right)}^2}=R\sqrt[]{2x-x^2}\mathrm{.}}\\ \hfill {\displaystyle V_2=\frac{R^2{\left(1-x\right)}^2\pi \cdot R\sqrt[]{2x-x^2}}{3}=\frac{R^3\pi }{3}\left({\left(1-x\right)}^2\sqrt[]{2x-x^2}\right)\mathrm{.}}\\ \hfill {\displaystyle V_1+V_2=\frac{R^3\pi }{3}\left(x^2\sqrt[]{1-x^2}+{\left(1-x\right)}^2\sqrt[]{2x-x^2}\right)\mathrm{.}}\end{array}}}\end{array}$ $\frac{R^3\pi }{3}$ pozitív állandó, így a maximum keresésekor elegendő vizsgálni az $\begin{array}{c}{\displaystyle f\left(x\right)=x^2\sqrt[]{1-x^2}+{\left(1-x\right)}^2\sqrt[]{2x-x^2}}\end{array}$ függvényt. Láttuk, hogy az $f\left(x\right)$ függvény értéke az $\alpha ={180}^{\circ }$, azaz $x=\mathrm{0,5}$ értékére $\mathrm{0,4330127}$. Azt kell eldöntenünk, van-e a függvénynek a $\left(\mathrm{0,}1\right)$ intervallumban ennél nagyobb értéke. A függvény ábrázolásához készíthetünk táblázatot, s ha a $\mathrm{0,5}$ környezetét vizsgáljuk, hamarosan találni fogunk nagyobb értéket. Legyen például $x=\mathrm{0,3}$, azaz $\alpha \approx {108}^{\circ }$, ekkor $\begin{array}{c}{\displaystyle f\left(\mathrm{0,3}\right)=\mathrm{0,}{3}^2\sqrt[]{1-\mathrm{0,}{3}^2}+{\left(1-\mathrm{0,3}\right)}^2\sqrt[]{\mathrm{0,6}-\mathrm{0,}{3}^2}\approx \mathrm{0,435779,}}\end{array}$ ami azt jelenti, hogy a körcikkekből formált tölcsérek össztérfogata $nem̲$ félkörök esetén lesz a legnagyobb.   Megjegyzés. A feladat kérdésére tagadó választ adhatunk akkor, ha találunk egy olyan szétvágást, amelynél a keletkezett térfogatok összege nagyobb, mint a felezéskor kapott kúpok térfogatának összege. A megoldók nagy része ezt az utat választotta. Többen azonban abba a hibába estek, hogy kiválasztottak egy felosztást, majd a kapott térfogatok összegét kisebbnek találva a felezéskor kapott térfogatnál, kijelentették, hogy valóban a felezéskor kapott térfogatok összege a legnagyobb. Látható a különbség: az állítás cáfolatához egyetlen példa elegendő, a bizonyításhoz azonban egyáltalán nem.   II. megoldás. A feladatot úgy is befejezhetjük, hogy az I. megoldás $f\left(x\right)$ függvényének megkeressük a maximumát. Csakhogy középiskolában tanult módszerekkel nemigen tudunk mit kezdeni a fenti $f\left(x\right)$ függvénnyel. Nézzük meg, hogyan oldható meg a feladat a Texas Instruments TI83 típusú grafikus számológépének segítségével: Az 1. ábra standard koordináta-rendszerben mutatja a függvény kirajzolt grafikonját. Látható, hogy az $x=\frac{1}{2}$ igen nagy környezetében mintha azonos lenne a függvényérték. Ha az $\left(\frac{1}{2};f\left(\frac{1}{2}\right)\right)$ pontra ,,zoom''-olunk, akkor egy lényegében vízszintes görbeszakaszt kapunk, a függvény olyan keveset változik, hogy ez nem elegendő a döntéshez: vajon $\frac{1}{2}$-nél van-e a maximum? A grafikus megoldás kulcslépése a 2. ábrán látható: változtassuk meg az $y$ koordinátatengely skálázását! Ekkor egyetlen gombnyomás után leolvasható a tagadó válasz (3. ábra), kiderül, hogy a függvény ,,középen behorpad'', a függvény nem az egyenlő sugarak esetén maximális.   1. ábra   2. ábra   3. ábra   4. ábra   Az már csak ráadás, hogy a kalkulátor a lokális maximumok értékét is meg tudja adni, ez látható a 4. ábrán. Mivel a számológép kerekítési hibáit is figyelembe kell vennünk, ajánlatos számolással újra ellenőriznünk, hogy $x=\mathrm{0,5}$ esetén valóban kisebb a függvényérték, mint $x=\mathrm{0,675}$ közelében.