Kezdőlap


Feladat:	C.569	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Besenyei Ádám , Zalán Péter
Füzet:	2000/október, 405. oldal		PDF \| MathML
Témakör(ök):	Gyökök és együtthatók közötti összefüggések, Parabola egyenlete, Kúpszeletek érintői, C gyakorlat
Hivatkozás(ok):	Feladatok: 2000/január: C.569

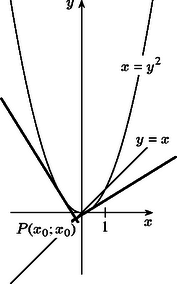
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $y = x^{2}$ egyenletű parabola tengelye az $y$ tengely, csúcsa pedig az origó. Az $y = x$ egyenes azon $P (x_{0}; x_{0})$ pontját keressük, amelyből a parabolához két egymásra merőleges érintő húzható.
Mivel a parabolának nincsen tengely irányú érintője, a $P$ -n átmenő érintőknek van iránytangense, egyenletük felírható

\begin{matrix} y - x_{0} = m (x - x_{0}) \end{matrix}

alakban. Ha egy ilyen egyenes érinti a parabolát, akkor pontosan egy közös pontjuk van. A parabola és egyenes közös pontjának koordinátái kielégítik mindkét görbe egyenletét. A két görbének akkor van egyetlen közös pontja, ha az egyenleteikből adódó másodfokú egyenlet diszkriminánsa 0, vagyis az

\begin{matrix} \begin{matrix} x^{2} - m x + (m - 1) x_{0} = 0 egyenletben \\ m^{2} - 4 x_{0} m + 4 x_{0} = 0, \end{matrix} \end{matrix}

ahonnan a gyökök és együtthatók közötti összefüggésből

m_{1} m_{2} = 4 x_{0}

.
Tudjuk továbbá, hogy az egymásra merőleges egyenesek iránytangenseinek szorzata

- 1

, vagyis

4 x_{0} = - 1

, innen

x_{0} = - \frac{1}{4}

. A keresett pont tehát a

P (- \frac{1}{4}; - \frac{1}{4})

Zalán Péter (Budapesti Evangélikus Gimn., 11. o.t.)

Megjegyzés. Besenyei Ádám (Tatabánya, Árpád Gimn., 12. o.t.) megmutatta, hogy az

y = a x^{2}

egyenletű parabola esetén azon pontok halmaza, amelyekből két egymásra merőleges érintő húzható a parabolához, egy egyenes, a parabola vezéregyenese. Ennek egyenlete

y = - \frac{1}{4 a}

. Ebből nyomban adódik feladatunk megoldása.