Kezdőlap


Feladat:	F.3277	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Székelyhidi Gábor , Terpai Tamás
Füzet:	2000/január, 27 - 28. oldal		PDF \| MathML
Témakör(ök):	Vektorok skaláris szorzata, Szabályos sokszögek geometriája, Helyvektorok, Aranymetszés, Feladat
Hivatkozás(ok):	Feladatok: 1999/március: F.3277

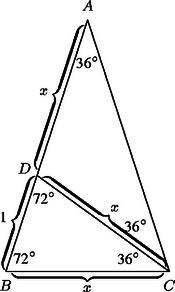
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldás során szükségünk lesz $cos 72^{\circ}$ és $cos 144^{\circ}$ pontos értékére. Ezeket az 1. ábrán látható $36^{\circ}$ -os szárszögű egyenlő szárú háromszög segítségével számoljuk ki. Használjuk az ábra jelöléseit. Az $A B C$ és a $C D B$ háromszögek hasonlóak, mert megfelelő szögeik egyenlők, ezért $(1 + x) : x = x : 1$ , amiből kapjuk, hogy $x = \frac{1 + \sqrt[]{5}}{2}$ , s így $A B = A C = \frac{3 + \sqrt[]{5}}{2}$ . Ezért

\begin{matrix} cos 72^{\circ} = \frac{\frac{B C}{2}}{A C} = \frac{\frac{1 + \sqrt[]{5}}{4}}{\frac{3 + \sqrt[]{5}}{2}} = \frac{\sqrt[]{5} - 1}{4}, \end{matrix}

amiből következik, hogy

cos 144^{\circ} = 2 cos^{2} 72^{\circ} - 1 = \frac{- 1 - \sqrt[]{5}}{4}

1. ábra

2. ábra

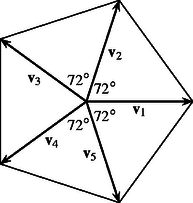
Térjünk rá az eredeti feladatra. Feltehetjük, hogy a

v_{1}

v_{2}

...

v_{5}

vektorok a 2. ábrán látható módon helyezkednek el, és mindegyikük hossza 1. Szorozzuk meg a

k_{1} v_{1} + k_{2} v_{2} + ... + k_{5} v_{5} = 0

egyenletet skalárisan a

v_{1}

vektorral. Ekkor kapjuk, hogy

\begin{matrix} k_{1} v_{1}^{2} + k_{2} v_{2} \cdot v_{1} + k_{3} v_{3} \cdot v_{1} + k_{4} v_{4} \cdot v_{1} + k_{5} v_{5} \cdot v_{1} = 0. \end{matrix}

\begin{matrix} v_{2} \cdot v_{1} = v_{5} \cdot v_{1} = cos 72^{\circ} és v_{3} \cdot v_{1} = v_{4} \cdot v_{1} = cos 144^{\circ}, \end{matrix}

tehát

\begin{matrix} k_{1} + (k_{2} + k_{5}) \cdot \frac{\sqrt[]{5} - 1}{4} + (k_{3} + k_{4}) \cdot \frac{- 1 - \sqrt[]{5}}{4} = 0, \end{matrix}

amit rendezve

\begin{matrix} 4 k_{1} - k_{2} - k_{3} - k_{4} - k_{5} = \sqrt[]{5} \cdot (k_{3} + k_{4} - k_{2} - k_{5}) \end{matrix}

adódik. Mivel a

k_{i}

-k egészek,

\sqrt[]{5}

pedig irracionális, ez csak akkor teljesülhet, ha

\begin{matrix} 4 k_{1} = k_{2} + k_{3} + k_{4} + k_{5} és k_{2} + k_{5} = k_{3} + k_{4} . \end{matrix}

Ezt a gondolatmenetet

v_{1}

helyett a

v_{i}

(

i = 2

, 3, 4, 5) vektorral megismételve azt kapjuk, hogy minden

i

esetén igaz az

5 k_{i} = k_{1} + k_{2} + ... + k_{5}

összefüggés, amiből nyilván következik, hogy

k_{1} = k_{2} = ... = k_{5}

Terpai Tamás (Fazekas M. Főv. Gyak. Gimn., 12. o.t.) dolgozata alapján

Megjegyzés. A feladat állítása általánosítható

5

-ről tetszőleges

p

-re, ahol

p

a 2-nél nagyobb prímszám. Ennek végsősoron az az oka, hogy minden ilyen

p

-re az

x^{p - 1} + x^{p - 2} + ... + x + 1

polinom irreducibilis, azaz nem bontható fel két olyan racionális együtthatós polinomnak a szorzatára, amelyeknek a foka legalább 1.