Kezdőlap


Feladat:	Gy.3284	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kovács Erika Renáta , Máthé András
Füzet:	2000/január, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Esetvizsgálat, Gyakorlat
Hivatkozás(ok):	Feladatok: 1999/május: Gy.3284

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítását körív helyett tetszőleges vonalra is belátjuk. Legyen $\tilde{A B}$ olyan vonal a kerület $A$ és $B$ pontjai között, amelyik felezi a kör területét. Ha $A$ és $B$ átellenes pontok a kör kerületén, akkor készen vagyunk, hiszen az $\tilde{A B}$ összekötés hosszabb, mint az 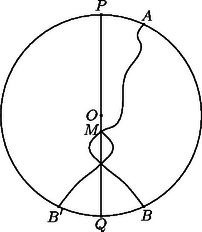$A B$ szakasz.

A

és

B

nem átellenes pontok, akkor tekintsük azt az ‐ egyetlen ‐

P Q

átmérőt, amelyik párhuzamos az

A B

szakasszal. (Ha

A

és

B

egybeesik, akkor legyen

P Q

A = B

-ben a körhöz húzott érintővel párhuzamos átmérő.)
Most

A

és

B

P Q

átmérőnek ugyanazon az oldalán vannak, így ha

\tilde{A B}

felezi a körlap területét, át kell mennie a

P Q

határolta másik félkörlapra is. Létezik tehát az

\tilde{A B}

vonalon olyan

M

pont, amely rajta van

P Q

-n. Tükrözzük

\tilde{M B}

-t

P Q

-ra, jelöljük ezt a vonalat

\tilde{M B'}

-vel! Ekkor

A

és

B'

átellenes pontok

k

-n, mert

{P A}_{}^{⌢} = {B Q}_{}^{⌢} = {Q B'}_{}^{⌢}

.
Ha az

\tilde{A M}

és az

\tilde{M B'}

vonalakat egymáshoz fűzzük, akkor egy

\tilde{A B'}

vonalat kapunk, ami legalább olyan hosszú ‐ valójában hosszabb ‐, mint az

A B'

átmérő, és ugyanolyan hosszú, mint

\tilde{A B}

. Ezzel a bizonyítást befejeztük.

Kovács Erika Renáta (Fazekas M. Főv. Gyak. Gimn., 9. o.t.) megoldása alapján