Feladat:	C.539	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Ábrány Miklós ,  Bérces Márton ,  Besenyei Ádám ,  Csató György ,  Fall Zoltán ,  Gajdos Béla ,  Gérecz Balázs ,  Király Péter ,  Lovas Róbert ,  Nagy Dávid ,  Pótó Júlia ,  Robotka Zsolt ,  Sapszon János ,  Szalay Zsófia ,  Szűcs Júlia
Füzet:	1999/december, 521 - 522. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometriával, Síkgeometriai bizonyítások, Derékszögű háromszögek geometriája, Thalesz tétel és megfordítása, C gyakorlat
Hivatkozás(ok):	Feladatok: 1999/április: C.539

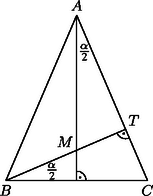
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az $ABC$ háromszögben ($AB=AC$) a $B$ csúcsból induló magasság talppontját jelöljük $T$-vel. Az $AMT$ háromszög hasonló $BTC$ háromszöghöz, mindkettő derékszögű, és $MAT\sphericalangle =TBC\sphericalangle =\frac{\alpha }{2}$, hiszen merőleges szárú hegyesszögek. A hasonlóság miatt $\begin{array}{c}{\displaystyle \frac{AM}{BC}=\frac{AT}{BT}\mathrm{,}\text{innen}AM=BC\cdot \frac{AT}{BT}\mathrm{.}}\end{array}$ (1) Tudjuk, hogy $BC=a$, az $ABT$ derékszögű háromszögből $\frac{AT}{BT}=\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\alpha$, ezeket helyettesítve (1)-be: $\begin{array}{c}{\displaystyle AM=a\cdot \text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\alpha =\frac{a}{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }\mathrm{,}}\end{array}$ amit bizonyítani akartunk.  Gérecz Balázs (Pannonhalma, Bencés Gimn., 10. o.t.)   II. megoldás. Rajzoljuk meg az $ABC$ egyenlő szárú háromszög ($AB=AC$) körülírt körét. 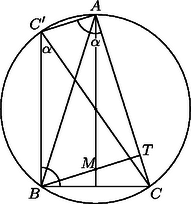A $C$ pont átellenes pontját a körön jelöljük $C\text{'}$-vel. A $C\text{'}BC$ háromszög derékszögű (Thálesz-tétel), és a kerületi szögek tétele szerint $BC\text{'}C\sphericalangle =\alpha$. A $C\text{'}AC$ szög ugyancsak derékszög, így $C\text{'}A\perp AC$ és $BT\perp AC$ miatt