Kezdőlap


Feladat:	F.3254	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baharev Ali , Dancsó Zsuzsanna , Dénes Attila , Győri Nikolett , Györey Bernadett , Harangi Viktor , Horváth Gábor , Horváth László , Kiss Gergely , Kunszenti-Kovács Dávid , Máthé András , Naszódi Gergely , Németh András , Pszota Anikó , Szabadka Zoltán , Szabó Péter , Székelyhidi Gábor , Szilasi Zoltán , Terpai Tamás , Vaik István , Vitéz Ildikó , Zábrádi Gergely
Füzet:	1999/október, 414 - 417. oldal		PDF \| MathML
Témakör(ök):	Geometriai transzformációk, Koordináta-geometria, Feladat
Hivatkozás(ok):	Feladatok: 1998/november: F.3254

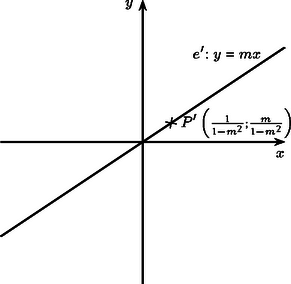
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $T$ -vel a megadott transzformációt. Először megmutatjuk, hogy $T$ inverze megegyezik $T$ -vel. Ehhez elegendő azt belátnunk, hogy ha $T$ -t egymás után kétszer alkalmazzuk, akkor minden pont képe önmaga. Ez nyilvánvaló azon pontok esetén, amelyek illeszkednek az $y = x$ vagy az $y = - x$ egyenletű egyenesekre. Legyen $Q (a, b)$ egy olyan pont, amelyre $| a | \neq | b |$ . Ekkor

\begin{matrix} \begin{matrix} T (T (Q (a, b))) & = T (Q' (\frac{a}{a^{2} - b^{2}}; \frac{b}{a^{2} - b^{2}})) = \\ = Q'' (\frac{\frac{a}{a^{2} - b^{2}}}{{(\frac{a}{a^{2} - b^{2}})}^{2} - {(\frac{b}{a^{2} - b^{2}})}^{2}}; \frac{\frac{b}{a^{2} - b^{2}}}{{(\frac{a}{a^{2} - b^{2}})}^{2} - {(\frac{b}{a^{2} - b^{2}})}^{2}}) . \end{matrix} \end{matrix}

Q''

pont koordinátáiban szereplő emeletes törteket átalakítva:

\begin{matrix} \frac{\frac{a}{a^{2} - b^{2}}}{{(\frac{a}{a^{2} - b^{2}})}^{2} - {(\frac{b}{a^{2} - b^{2}})}^{2}} = \frac{a (a^{2} - b^{2})}{a^{2} - b^{2}} = a és \frac{\frac{b}{a^{2} - b^{2}}}{{(\frac{a}{a^{2} - b^{2}})}^{2} - {(\frac{b}{a^{2} - b^{2}})}^{2}} = \frac{b (a^{2} - b^{2})}{a^{2} - b^{2}} = b, \end{matrix}

tehát

Q''

valóban megegyezik

Q

-val.
Ha a síkon egy

A

alakzat egyenlete

F (x, y) = 0

S

pedig olyan invertálható transzformáció, amelynek

S^{- 1}

inverze a

P (x, y)

pontot a

P' (x', y')

pontba viszi, akkor az

A

alakzat

S

-nél származó képének egyenlete

F (x', y') = 0

, mert

P \in S (A)

pontosan akkor teljesül, ha

S^{- 1} (P) \in S^{- 1} (S (A))

, azaz ha

P' \in A

.
Esetünkben

T^{- 1} = T

, tehát a transzformáció inverze is helyben hagyja azokat a pontokat, amelyeknek koordinátáira

| x | = | y |

teljesül,

| x | \neq | y |

esetén pedig

T^{- 1} (P (x, y)) = P' (\frac{x}{x^{2} - y^{2}}; \frac{y}{x^{2} - y^{2}})

. A sík minden

e

egyenesének egyenlete felírható

A x + B y + C = 0

alakban, ahol

A^{2} + B^{2} \neq 0

. Az

e

egyenesnek azok a pontjai, amelyek rajta vannak az

y = x

vagy az

y = - x

egyenletű egyeneseken, helyben maradnak a

T

transzformációnál, az

e

további pontjai pedig az előzőek alapján az

\begin{matrix} A \frac{x}{x^{2} - y^{2}} + B \frac{y}{x^{2} - y^{2}} + C = 0 \end{matrix}

egyenletű alakzatra kerülnek. E pontok megegyeznek a

\begin{matrix} C (x^{2} - y^{2}) + A x + B y = 0 \end{matrix}

(1)

egyenletű alakzat pontjaival. Az (1) egyenlet

C = 0

esetén

A^{2} + B^{2} \neq 0

miatt egy origón átmenő egyenes egyenlete. Ha

C \neq 0

, akkor (1) a következő alakra hozható:

\begin{matrix} {(x + \frac{A}{2 C})}^{2} - {(y - \frac{B}{2 C})}^{2} = \frac{A^{2} - B^{2}}{4 C^{2}} . \end{matrix}

(2)

| A | \neq | B |

esetén egy hiperbola,

| A | = | B |

esetén pedig egy metsző egyenespár egyenlete.
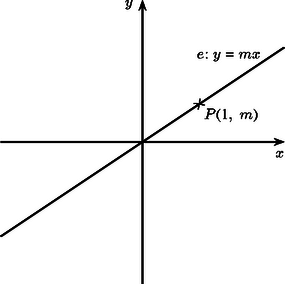
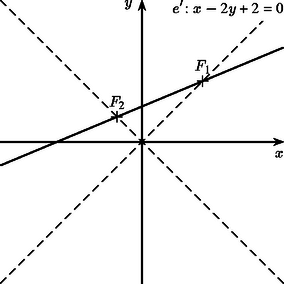
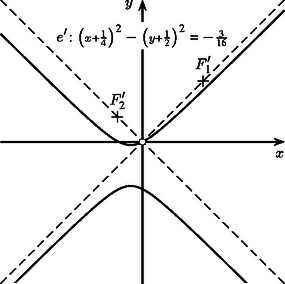
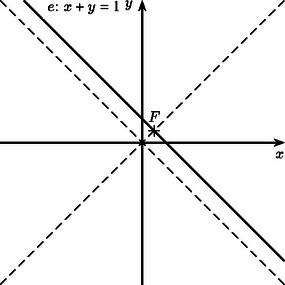
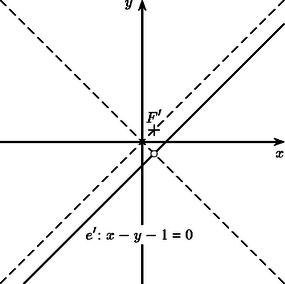
Ezek alapján a sík egyeneseinek

T

-nél kapott képe a következő:
i) Ha

e

egy origón átmenő egyenes, akkor képe önmaga (1. ábra). Ha egyenlete

y = \pm x

, akkor a képe

T

definíciója szerint önmaga. Ha pedig egyenlete

A x + B y = 0

, akkor

C = 0

miatt az (1) egyenlet, tehát

e

képének egyenlete is

A x + B y = 0

, és ennek az egyenesnek minden pontja előáll képként.
ii) Ha

e

nem megy át az origón és nem párhuzamos az

y = \pm x

egyenletű egyenesek egyikével sem ‐ azaz ha

C \neq 0

és

| A | \neq | B |

‐, akkor

e

-nek az

y = \pm x

egyenletű egyenesekkel való metszéspontjai helyben maradnak, a további pontok képei pedig a (2) egyenletű hiperbolának az origótól különböző összes pontját befutják (2. ábra).
iii) Ha

e

nem megy át az origón, de párhuzamos az

y = \pm x

egyenletű egyenesek egyikével ‐ azaz ha

C \neq 0

és

| A | = | B |

‐, akkor a (2) egyenlet

\begin{matrix} (x + y + \frac{A - B}{2 C}) (x - y + \frac{A + B}{2 C}) = 0 \end{matrix}

(3)

alakba írható.

| A | = | B |

miatt a két egyenes egyike megegyezik az

y = \pm x

egyenesek egyikével. Az

e

egyenes képe a (3) egyenlettel leírt egyenespár másik egyenese lesz, kivéve a 3. ábrán látható metszéspontot. Ezen kívül ebben az esetben is lesz egy fixpont,

e

-nek az

y = x

vagy az

y = - x

egyenletű egyenessel való metszéspontja.

Szilasi Zoltán (Debrecen, KLTE Gyak. Gimn., 10. o.t.) dolgozata alapján