Kezdőlap


Feladat:	C.532	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Csató György , Gajdos Béla , Gueth Krisztián , Kalcsú Áron , Robotka Zsolt
Füzet:	1999/október, 401 - 402. oldal		PDF \| MathML
Témakör(ök):	Csonkakúp, Terület, felszín, C gyakorlat
Hivatkozás(ok):	Feladatok: 1999/február: C.532

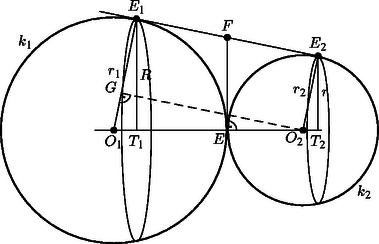
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $k_{1}$ , $k_{2}$ körök középpontját jelöljük $O_{1}$ és $O_{2}$ -vel, sugarát $r_{1}$ és $r_{2}$ -vel, és legyen $r_{1} \geq r_{2}$ . A két kör közös pontja $E$ , az érintési pontok $k_{1}$ -en $E_{1}$ , $k_{2}$ -n $E_{2}$ . $E_{1}$ és $E_{2}$ merőleges vetülete az $O_{1} O_{2}$ centrálisra $T_{1}$ , illetve $T_{2}$ . A forgatáskor keletkezett csonkakúp alapköreinek sugarai $E_{1} T_{1} = R$ , $E_{2} T_{2} = r$ , palástjának alkotója $E_{1} E_{2} = a$ .
Ismeretes, hogy a csonkakúp palástjának területe:

\begin{matrix} P = π (R + r) a . \end{matrix}

(1)

Mivel

O_{1} E_{1}

és

O_{2} E_{2}

merőlegesek

E_{1} E_{2}

-re, ha

O_{2}

-ből párhuzamost húzunk

E_{1} E_{2}

-vel, amelynek metszéspontja

O_{2} E_{2}

-vel

G

, akkor

O_{1} O_{2} = r_{1} + r_{2}

és

O_{1} G = r_{1} - r_{2}

, így az

O_{2} G O_{1}

derékszögű háromszögből

\begin{matrix} a = E_{1} E_{2} = O_{2} G = \sqrt[]{{(r_{1} + r_{2})}^{2} - {(r_{1} - r_{2})}^{2}} = \sqrt[]{4 r_{1} r_{2}} . \end{matrix}

(2)

T_{1} T_{2} E_{2} E_{1}

derékszögű trapézban a szárak:

E_{1} T_{1} = R

és

E_{2} T_{2} = r

. Messe az

E

-ben húzott közös érintő az

E_{1} E_{2}

egyenest

F

-ben. Tudjuk, hogy egy külső pontból a körhöz húzott érintőszakaszok hossza egyenlő, azért

F E_{1} = F E = F E_{2}

F E

merőleges

O_{1} O_{2}

-re, vagyis

F E

a trapéz középvonala:

\begin{matrix} \frac{R + r}{2} = F E = F E_{2} = F E_{1} . \end{matrix}

Azt kaptuk, hogy

R + r

egyenlő az alkotóval,

E_{1} E_{2}

-vel.

E_{1} E_{2} = R + r = \sqrt[]{4 r_{1} r_{2}}

, és (1)-be helyettesítve:

\begin{matrix} P = π (R + r) a = π \sqrt[]{4 r_{1} r_{2}} \cdot \sqrt[]{4 r_{1} r_{2}} = 4 π r_{1} r_{2} . \end{matrix}

Gajdos Béla (Ukrajna, Beregszász, Bethlen G. Gimn., 11. o.t.)

Megjegyzés. A megoldás során lényegében azt láttuk be, hogy mind a körök közös

E_{1} E_{2}

érintője, mind pedig az

R + r

összeg egyenlő a két kör átmérőjének a mértani közepével.