Kezdőlap


Feladat:	F.3196	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bárány Kristóf , Barát Anna , Bíró Zsuzsanna , Dályay Virág , Gueth Krisztián , Gyenes Zoltán , Hartmann Miklós , Hegedűs Péter , Juhász András , Léka Zoltán , Lippner Gábor , Lukács László , Mansur Boase , Pataki Péter , Pogány Ádám , Terpai Tamás , Vaik Zsuzsanna , Végh A. László
Füzet:	1999/január, 30 - 32. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus függvények, Számsorozatok, Függvényvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 1997/november: F.3196

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először belátjuk, hogy $cos x < \frac{1}{\sqrt[]{1 + x^{2}}}$ , ha $0 < x < \frac{π}{2}$ . Mivel $0 < x < \frac{π}{2}$ esetén $sin x < x < tg x$ , azért

\begin{matrix} cos x \cdot \sqrt[]{1 + x^{2}} < cos x \cdot \sqrt[]{1 + tg^{2} x} = \sqrt[]{cos^{2} x + sin^{2} x} = 1, \end{matrix}

tehát valóban

cos x < \frac{1}{\sqrt[]{1 + x^{2}}}

.
Ezek után

n

-re vonatkozó indukcióval igazoljuk, hogy amennyiben

n \geq 1

, akkor

0 < a_{n} < 2 \cdot \sqrt[]{\frac{1}{n}}

n = 1

esetén:

0 < a_{1} = sin 1 \leq 1 < 2 \cdot \sqrt[]{\frac{1}{1}} = 2

n = 2

-re

0 < sin (sin 1) < 2 \sqrt[]{\frac{1}{2}} = \sqrt[]{2}

.
Legyen

k \geq 2

, és tegyük fel, hogy

k

-ig minden természetes számra igaz a fenti állítás.
Nyilván

sin a_{k} < sin 2 \cdot \sqrt[]{\frac{1}{k}}

, mivel

a_{k} < 2 \sqrt[]{\frac{1}{k}}

, a szinuszfüggvény szigorúan monoton növekvő a

[0, \frac{π}{2}]

intervallumban, végül

0 < a_{k} < 2 \cdot \sqrt[]{\frac{1}{k}} < \frac{π}{2}

. Felhasználva a

sin x < x

és a

cos x < \frac{1}{\sqrt[]{1 + x^{2}}}

egyenlőtlenségeket, kapjuk, hogy:

\begin{matrix} \begin{matrix} 0 & < a_{k + 1} = sin a_{k} < sin 2 \cdot \sqrt[]{\frac{1}{k}} = 2 sin \sqrt[]{\frac{1}{k}} cos \sqrt[]{\frac{1}{k}} < 2 \sqrt[]{\frac{1}{k}} \cdot \frac{1}{\sqrt[]{1 + \frac{1}{k}}} = 2 \cdot \frac{1}{\sqrt[]{k + 1}} . \end{matrix} \end{matrix}

Vagyis, ha

n = k

esetén igaz az állítás, akkor

n = k + 1

esetén is. Így minden

n > 1

-re

0 < a_{n} < 2 \cdot \sqrt[]{\frac{1}{n}}

. Ebből

0 < n a_{n}^{2} < 4

, az

n a_{n}^{2}

sorozat tehát valóban korlátos.

Megjegyzések. 1. A megoldás során nem bizonyítottuk a

sin x < x < tg x

egyenlőtlenséget. Ez persze csak akkor áll fenn, ha

0 < x < \frac{π}{2}

.
Vegyük az egységsugarú kört és benne az

x

nagyságú középponti szöget.
Használjuk az ábra jelöléseit: az

A B

körív hossza

x

B B' = sin x

A A' = tg x

. Az

A B

körív hosszabb, mint az

A B

szakasz. Így

A B > B B'

miatt

x > sin x

. Az

A O A'

háromszög területe nagyobb, mint az

A O B

körcikk területe. Tehát:

\begin{matrix} \frac{tg x}{2} = \frac{O A \cdot A A'}{2} > \frac{A O^{2} \cdot A O B ∢}{2} = \frac{x}{2} . \end{matrix}

Összefoglalva:

sin x < x < tg x

.
2. Körülményesebb úton a talált felső korlát javítható. Többen igazolták, hogy

0 < n a_{n}^{2} < 3

is teljesül. Hegedűs Péter (Miskolc, Földes F. Gimn., 11. o.t.) amellett, hogy bebizonyította az élesített egyenlőtlenséget, felhívta figyelmünket, hogy Pólya György‐Szegő Gábor: Feladatok és tételek az analízis köréből I. című könyvében (Tankönyvkiadó, 1980) a II. fejezet 173. feladata szerint, ha

sin x > 0

, akkor a

sin_{1} x = sin x

sin_{n} x = sin (sin_{n - 1} x)

iterációval megadott sorozatra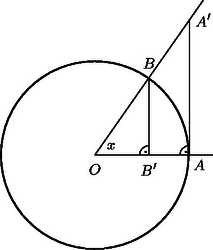

\begin{matrix} {lim}_{}^{}_{n \to \infty}^{} \sqrt[]{\frac{n}{3}} sin_{n} x = 1. \end{matrix}

Eszerint a feladatban megadott

n a_{n}^{2}

sorozat nemcsak korlátos, hanem konvergens is, és a határértéke 3. Ez pedig azt jelenti, hogy ez a felső korlát már nem javítható tovább.